|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАТРИЦ АЛГЕБРАЗначение МАТРИЦ АЛГЕБРА в математической энциклопедии: матричная алгебра,- подалгебра полной матричной алгебры Fn всех
для Алгебра Fn изоморфна алгебре всех эндоморфизмов n-мерного линейного пространства над F. Размерность Fn ' над Fравна n2. Любая ассоциативная алгебра с единицей, размерность к-рой над Fне больше п, изоморфна нек-рой подалгебре в Fn. Ассоциативная алгебра без единицы, размерности меньше пнад F, также изоморфно вкладывается в F п. В силу теоремы Веддерберна алгебра Fn проста, т. е. имеет лишь тривиальные двусторонние идеалы. Центр алгебры Fn состоит из всех скалярных
Неприводимая М. а. проста. Если М. а. Аабсолютно неприводима (напр., когда поле Fалгебраически замкнуто), то A = Fn при n>1 (теорема Бёрнсайда). М. а. полупроста тогда и только тогда, когда она вполне приводима. С точностью до сопряженности в Fn имеется единственная максимальная нильпотентная подалгебра - алгебра всех верхних треугольных матриц с нулевой диагональю. В алгебре F п тогда и только тогда имеется коммутативная подалгебра размерности r, когда
(теорема - Шура). Для поля комплексных чисел С множество классов сопряженных максимальных коммутативных подалгебр алгебры В алгебре Fn выполняется стандартное тождество степени 2n:
где S2n- симметрич. группа, и никакое тождество меньшей степени не выполняется. Лит.:[l] Вейль Г., Классические группы, их инварианты и лредставленип, пер. с англ., М., 1947; [2] Джекобсон Н., Строение колец, пер. с англ., М.. 1961; [3] Херстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [4] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [5] Супруненко Д. А., Тышкевич Р. И., Перестановочные матрицы, Минск, 1966. Д. Л. Супруненко. |
|
|
|

 -матриц над полем F. Операции в Fn определяются следующим образом:
-матриц над полем F. Операции в Fn определяются следующим образом: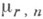

 -матриц над F. Группа обратимых элементов алгебры Fn есть полная линейная группа
-матриц над F. Группа обратимых элементов алгебры Fn есть полная линейная группа 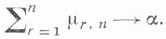 Каждый автоморфизм hалгебры Fn является внутренним:
Каждый автоморфизм hалгебры Fn является внутренним:
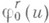
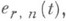 при
при  конечно, а при n>6 бесконечно.
конечно, а при n>6 бесконечно.