|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯЗначение МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ в математической энциклопедии: - уравнения, описывающие математические модели физических явлений. М. ф. у.- часть предмета математической физики. Многие явления физики и механики (гидро- и газодинамики, упругости, электродинамики, оптики, теории переноса, физики плазмы, квантовой физики, теории гравитации и т. д.) описываются краевыми задачами для дифференциальных уравнений. Эти задачи составляют весьма широкий класс М. ф. у. Для полного описания эволюции физич. процесса, помимо уравнений, необходимо, во-первых, задать картину процесса в нек-рый фиксированный момент времени (начальные условия) и, во-вторых, задать режим на границе той среды, где протекает этот процесс (граничные условия). Начальные и граничные условия образуют краевые условия, а дифференциальные уравнения вместе с соответствующими краевыми условиями - краевую задачу математич. физики. Ниже приведены нек-рые примеры уравнений и соответствующих краевых задач. Уравнение колебаний
описывает малые колебания струн, стержней, мембран, акустические и электромагнитные колебания. В уравнении (1) пространственные переменные процесс; при этом в соответствии с физич. смыслом входящих величин должно быть Кроме того, полагают При
где Уравнение диффузии
описывает процессы диффузии частиц и распространения тепла в среде. Уравнение (3) - параболического типа уравнение. При уравнение (3) превращается в теплопроводности уравнение Для стационарных процессов, когда отсутствует зависимость от времени t, уравнения колебаний (1) и диффузии (3) принимают вид
Уравнение (5) - эллиптического типа уравнение. При а при
Уравнениям (6) и (7) удовлетворяют различного рода потенциалы: ньютонов (кулонов) потенциал, потенциал течения несжимаемой жидкости и т. д. Если в волновом уравнении (2) внешнее возмущение f- периодическое с частотой w,
то амплитуда
удовлетворяет Гелъмгольца уравнению
К уравнению Гельмгольца приводят задачи на рассеяние (дифракцию). Для полного описания процесса колебаний необходимо задать начальное возмущение и начальную скорость
а для процесса диффузии - только начальное возмущение Кроме того, на границе Sобласти Gнеобходимо удовлетворить заданному режиму. В простейших случаях физически осмысленные граничные условия для уравнений (1), (3), (5) описываются соотношением
где ки h- заданные неотрицательные функции, не обращающиеся в нуль одновременно, п- внешняя нормаль к поверхности Sи v- заданная функция. Напр., для струны условие
означает, что конец струны
означает, что конец х 0 свободен. Для теплопроводности условие
означает, что на границе Sобласти Gподдерживается заданный температурный режим, а условие
задает поток тепла через S. В случае неограниченных областей, напр, внешности ограниченной области,, кроме условия на границе задается также условие на бесконечности. Так, для уравнения Пуассона (6) в пространстве (n=3) таким условием является условие а на плоскости ( п=2)- условие
Для уравнения Гельмгольца (8) на бесконечности задаются излучения условия Зоммерфельда
причем знак "-" соответствует расходящимся, а знак "+"- сходящимся волнам. Краевая задача, к-рая содержит только начальные условия (и стало быть, не содержит граничных условий, так что область G- все пространство Rn), наз. Ноши задачей. Для уравнения колебаний (1) задача Коши (1), (9) ставится следующим образом: найти функцию и( х, t )класса Если в краевой задаче присутствуют и начальные и граничные условия, то такая задача наз. смешанной задачей. Для уравнения колебаний (1) смешанная задача (1), (9), (11) ставится так: найти функцию и( х, t )класса
удовлетворяющую уравнению (1) в цилиндре Для стационарного уравнения (5) начальные условия отсутствуют и соответствующая краевая задача ставится так: найти функцию удовлетворяющую уравнению (5) в области Gи граничному условию на границе S области G:
Для уравнения (5) краевая задача с граничным условием
наз. Дирихле задачей, а с граничным условием
- Неймана задачей. Различают внешние и внутренние краевые задачи Дирихле и Неймана. Для внешних -задач кроме граничных условий необходимо задавать условия на бесконечности типа (14), (15), (16). К краевым задачам для уравнения (5) относятся также задачи на собственные значения: найти те значения параметра
имеет нетривиальные решения (собственные функции), удовлетворяющие однородному граничному условию
Если G - ограниченная область с достаточно гладкой границей S, то существует счетное число неотрицательных собственных значений Изложенные постановки краевых задач предполагают достаточную гладкость решения как внутри области, так и вплоть до границы. Такие постановки краевых задач наз. классическими. Однако во многих физически интересных задачах приходится отказываться от таких требований гладкости. Внутри области решение может быть обобщенной функцией и удовлетворять уравнению в смысле обобщенных функций, краевые условия могут удовлетворяться в каком-либо обобщенном смысле (почти везде, в L р, в слабом смысле и т. д.). Такие постановки краевых задач наз. обобщенными постановками, а соответствующие решения - обобщенными решениями. Напр., обобщенная задача Коши для волнового уравнения ставится следующим образом. Пусть и- классич. решение задачи Коши (2), (9). Функции uи f продолжаются нулем на t<0 и обозначаются через
При этом начальные возмущения и 0 и и 1 играют роль мгновенно действующих внешних источников типа двойного слоя,
к-рые обращаются в нуль при t<0. Аналогично ставится обобщенная задача Коши и для уравнения теплопроводности (4). Поскольку краевые задачи математич. физики описывают реальные физич. процессы, то они должны удовлетворять следующим естественным требованиям, сформулированным Ж. Адамаром (J. Hadamard). 1) Решение должно существовать в нек-ром классе функций М 1 . 2) Решение должно быть единственным в, возможно, другом классе функций М 2 . 3) Решение должно непрерывно зависеть от данных задачи (начальных и граничных данных, свободных членов, коэффициентов уравнения и т. д.). Требование непрерывной зависимости решения возникает в связи с тем, что данные физич. задачи, как правило, определяются из эксперимента приближенно, и поэтому необходимо быть уверенным в том, что решение задачи не будет существенно зависеть от погрешностей измерений этих данных. Задача, удовлетворяющая перечисленным требованиям 1)-3), наз. корректно поставленной, а множество функций Нахождение корректных постановок краевых задач математич. физики и методов построения их решений (точных или приближенных) и составляет одно из главных содержаний предмета М. ф. у. Известно, что все перечисленные выше краевые задачи поставлены корректно. Пример. Задача Коши Задача, не удовлетворяющая хотя бы одному из условий 1)-3), наз. некорректной задачей. Некорректные задачи приобретают в современной математич. физике все возрастающее значение: сюда в первую очередь относятся обратные задачи, а также задачи, связанные с обработкой и интерпретацией результатов наблюдений. Примером некорректно поставленной задачи может служить задача Коши для уравнения Лапласа (пример Адамара):
Решение
однако
Для приближенного решения некорректных задач существует регуляризации метод, использующий дополнительную информацию о решении и сводящийся к решению ряда корректно поставленных задач. Важную роль в М. ф. у. играет понятие Грина функции. Функцией Грина линейного дифференциального оператора
с заданными (однородными) краевыми условиями на границе области изменения переменных ( х, t )наз. функция
В физич. ситуациях функция Грина
Доказано существование фундаментального решения из D' и S' для любого оператора Примеры фундаментальных решений. Волновое уравнение
где
Уравнение теплопроводности:
Уравнение Лапласа:
С помощью фундаментального решения Е( х, t )решение и( х, t )уравнения
с произвольной правой частью
если она существует в D'. В физич. ситуациях смысл формулы (22) следующий: это есть суммарное наложение элементарных возмущений В частности, решения обобщенной задачи Коши для волнового уравнения (и уравнения теплопроводности) выражается волновым (тепловым) потенциалом Из формулы (22') при надлежащих предположениях о гладкости источника
следуют классич. формулы решения задач Коши. Напр., для волнового уравнения в пространстве - Кирхгофа формула:
Для уравнения теплопроводности - Пуассона формула:
Таким же путем, строя функцию Грина для уравнения Лапласа для шара, получают решение внутренней задачи Дирихле для (трехмерного) шара
Для исследования и приближенного решения смешанных задач используется Фурье метод (разделения переменных) при условии, что коэффициенты в уравнении и в граничном условии не зависят от времени t. Идея метода, применительно, напр., к задаче (3), (10), (18) состоит в следующем: искомое решение правая часть
Подставляя формально эти ряды в уравнение (3), для неизвестных функций
При этом, чтобы ряд (26) для иудовлетворял начальному условию (10), необходимо положить
Решая задачу Коши (27), (28), получают формальное решение задачи (3), (10), (18) в виде ряда:
Возникает задача обоснования метода Фурье: когда формальный ряд (29) даст классическое или обобщенное решение задачи (3), (10), (18)? При обосновании метода Фурье и, вообще, при установлении корректности смешанной задачи для уравнения диффузии (3) используется максимума принцип. Аналогично метод Фурье применяется и к смешанной задаче (1), (9), (18) для уравнения колебаний. В этом случае оказывается полезным метод энергии интеграла. Метод разделения переменных находит применение также и для решения краевых задач для уравнения эллиптич. типа (5), в частности для вычисления собственных функций и собственных значений при условии, что область Gобладает достаточной симметрией. Для исследования и приближенного решения краевых задач для уравнения (5) широко используются вариационные методы. Так, напр., для задачи на собственные значения (17), (18) (при
где функции сравнения При исследовании краевых задач для уравнения (5) (в частности, для гармонич. функций) применяется принцип максимума. Перечисленные краевые задачи далеко не исчерпывают все многообразие краевых задач математич. физики - это есть простейшие классич. примеры краевых задач. Краевые задачи, описывающие реальные физич. процессы, могут быть весьма сложными: это могут быть системы уравнений, уравнения высших порядков, нелинейные уравнения. Сюда в первую очередь относятся: уравнение Шрёдингера, уравнения гидродинамики, переноса, магнитной гидродинамики, уравнения Максвелла, теории упругости, уравнения Дирака, уравнения Эйнштейна, уравнения Янга - Миллса и др. В связи с поисками нетривиальных моделей, описывающих взаимодействие квантовых нолей, возрос интерес к классическим нелинейным уравнениям:
- Кортевега- де Фриса уравнение;
-нелинейное волновое уравнение (Лиувилля при
- нелинейное уравнение Шрёдингера. Характерной чертой таких уравнений является наличие решений типа "уединенной волны" ( солитонов). Напр., для уравнения (31) таким решением является
Это решение обладает конечной энергией. Лит.:[1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 5 изд., М., 1977; [2] Владимиров В. С, Уравнения математической физики, 4 изд.,М., 1981; [3] Тихонов А. Н., Арсенин В. Я., Методы решения некорректных задач, М., 1974; [4] Xермандер. Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [5] Адамар Ж., Задача Коши для линейных уравнений с частными производными гиперболического типа, пер. с франц., М., 1978; [6] Уизем Д ж., Линейные и нелинейные волны, пер. с англ., М., 1977; [7] Михаилов В. П., Дифференциальные уравнения в частных производных, М., 1976; [8] Ладыженская О. А., Краевые задачи математической физики, М., 1973; [9] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., 2 изд., т. 2, М.-Л., 1951; [10] Владимиров В. С, Обобщенные функции в математической физике, 2 изд., М., 1979. В. С. Владимиров. |
|
|
|



 изменяются в области
изменяются в области  ,
,
 где развивается рассматриваемый физич.
где развивается рассматриваемый физич.
 . При этих условиях уравнение (1) - гиперболического типа уравнение.
. При этих условиях уравнение (1) - гиперболического типа уравнение. уравнение (1) превращается в волновое уравнение
уравнение (1) превращается в волновое уравнение
 - оператор Лапласа.
- оператор Лапласа.



 уравнение (5) наз. Пуассона уравнением:
уравнение (5) наз. Пуассона уравнением: - Лапласауравнением
- Лапласауравнением


 периодич. решения с той же частотой w
периодич. решения с той же частотой w





 закреплен, а условий
закреплен, а условий





 , удовлетворяющую уравнению (1) при i>0 и начальным условиям (9) на плоскости t=0. Аналогично ставится и задача Коши (3), (10) для уравнения диффузии (3).
, удовлетворяющую уравнению (1) при i>0 и начальным условиям (9) на плоскости t=0. Аналогично ставится и задача Коши (3), (10) для уравнения диффузии (3).
 , начальным условиям (9) на его нижнем основании
, начальным условиям (9) на его нижнем основании  и граничному условию (11) на его боковой поверхности
и граничному условию (11) на его боковой поверхности  . Аналогично ставится смешанная задача (3), (10), (11) для уравнения диффузии (3). Существуют и другие постановки краевых задач, напр. Гурса задача, Трикоми задача.
. Аналогично ставится смешанная задача (3), (10), (11) для уравнения диффузии (3). Существуют и другие постановки краевых задач, напр. Гурса задача, Трикоми задача. класса
класса 



 (собственные значения), при к-рых однородное уравнение
(собственные значения), при к-рых однородное уравнение

 задачи {17), (18)
задачи {17), (18)  каждое
каждое  - конечной кратности, соответствующие собственные функции
- конечной кратности, соответствующие собственные функции  образуют полную ортонормированную систему функций в
образуют полную ортонормированную систему функций в  ; при этом всякая функция класса
; при этом всякая функция класса  , удовлетворяющая граничному условию (18), разлагается в регулярно сходящийся ряд Фурье по системе собственных функций {uk}.
, удовлетворяющая граничному условию (18), разлагается в регулярно сходящийся ряд Фурье по системе собственных функций {uk}. соответственно. Тогда функция ибудет удовлетворять в смысле обобщенных функций во всем пространстве
соответственно. Тогда функция ибудет удовлетворять в смысле обобщенных функций во всем пространстве  волновому уравнению
волновому уравнению
 и простого слоя,
и простого слоя,
 . Сказанное позволяет ввести следующее определение. Обобщенной задачей Коши для волнового уравнения с источником
. Сказанное позволяет ввести следующее определение. Обобщенной задачей Коши для волнового уравнения с источником  F=0 при t<0, наз. задача об отыскании тех обобщенных решений
F=0 при t<0, наз. задача об отыскании тех обобщенных решений  волнового уравнения
волнового уравнения
 - классом корректности. Хотя требования 1)-3) на первый взгляд кажутся естественными, их, тем не менее, необходимо доказывать в рамках принятой математич. модели. Доказательство корректности - это первая апробация математич. модели,- модель непротиворечива, не содержит паразитных решений и мало чувствительна к погрешностям измерений.
- классом корректности. Хотя требования 1)-3) на первый взгляд кажутся естественными, их, тем не менее, необходимо доказывать в рамках принятой математич. модели. Доказательство корректности - это первая апробация математич. модели,- модель непротиворечива, не содержит паразитных решений и мало чувствительна к погрешностям измерений. поставлена корректно, если
поставлена корректно, если  .
. 



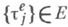 удовлетворяющая при каждом
удовлетворяющая при каждом из этой области уравнению
из этой области уравнению
 описывает возмущение от точечного (в точке
описывает возмущение от точечного (в точке  ) мгновенного (в момент
) мгновенного (в момент 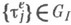 ) источника интенсивности 1 (с учетом неоднородности среды и краевого эффекта). В случае постоянных коэффициентов и отсутствия границы функция Грина при
) источника интенсивности 1 (с учетом неоднородности среды и краевого эффекта). В случае постоянных коэффициентов и отсутствия границы функция Грина при  наз. фундаментальным решением и обозначается Е( х, t).
наз. фундаментальным решением и обозначается Е( х, t).


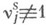 - функция Хевисайда:
- функция Хевисайда:  при
при  ;
; при
при  .
. 


 выражается во всем пространстве
выражается во всем пространстве  сверткой
сверткой
 от точечных источников
от точечных источников  на к-рые разлагается источник
на к-рые разлагается источник  в силу тождества
в силу тождества  . При этом свертка F* Еиграет роль соответствующего потенциала с источником (плотностью) F. В этом состоит сущность метода точечного источника решения линейных задач математич. физики.
. При этом свертка F* Еиграет роль соответствующего потенциала с источником (плотностью) F. В этом состоит сущность метода точечного источника решения линейных задач математич. физики.



 в виде Пуассона интеграла:
в виде Пуассона интеграла:
 и
и  разлагаются в ряд Фурье по собственным функциям
разлагаются в ряд Фурье по собственным функциям  краевой задачи (17), (18)
краевой задачи (17), (18)
 получают уравнение:
получают уравнение:


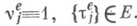 ) собственные значения
) собственные значения  удовлетворяют вариационному принципу:
удовлетворяют вариационному принципу:
 предполагаются из класса
предполагаются из класса  и удовлетворяют граничному условию (18); при этом inf в (30) реализуется на любой собственной функции, соответствующей собственному значению lk, и только на них.
и удовлетворяют граничному условию (18); при этом inf в (30) реализуется на любой собственной функции, соответствующей собственному значению lk, и только на них.

 ; Sine-Гордона при
; Sine-Гордона при  );
);
