|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАТЕМАТИЧЕСКИЙ АНАЛИЗЗначение МАТЕМАТИЧЕСКИЙ АНАЛИЗ в математической энциклопедии: часть математики, в к-рой функции и их обобщения изучаются методом пределов. Понятие предела тесно связано с понятием бесконечно малой величины, поэтому можно также сказать, что М. а. изучает функции и их обобщения методом бесконечно малых. Название "М. а." - сокращенное видоизменение старого названия этой части математики - "Анализ бесконечно малых"; последнее полнее раскрывает содержание, но оно - тоже сокращенное (название "Анализ посредством бесконечно малых" охарактеризовало бы предмет более точно). В классическом М. а. объектами изучения (анализа) являются прежде всего функции. "Прежде всего" потому, что развитие М. а. привело к возможности изучения его методами более сложных образований, чем функция, - функционалов, операторов и т. д. В природе и технике всюду встречаются движения, процессы, к-рые описываются функциями; законы явлений природы также обычно описываются функциями. Отсюда объективная важность М. а. как средства изучения функций. М. а. в широком понимании этого термина охватывает весьма большую часть математики. В него входят дифференциальное исчисление, интегральное исчисление, функций действительного переменного теория, функций комплексного переменного теория, приближения теория, теория дифференциальных уравнений обыкновенных, теория дифференциальных уравнений с частными производными, теория интегральных уравнений, дифференциальная геометрия, вариационное исчисление, функциональный анализ и нек-рые другие математич. дисциплины. Современные чисел теория и вероятностей теория применяют и развивают методы М. а. Все же термин М. а. часто употребляется для наименования только основ математического анализа, объединяющих в себе теорию действительного числа, теорию пределов, теорию рядов, дифференциальное и интегральное исчисление и их непосредственные приложения, такие как теория максимумов и минимумов, теория неявных функций, Фурье ряды, Фурье интегралы. Функция. В М. а. исходят из определения функции по Лобачевскому и Дирихле. Если каждому числу хиз нек-рого множества Fчисел в силу к.-л. закона приведено в соответствие число у, то этим определена функция 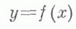 от одного переменного х. Аналогично определяется функция  от ппеременных, где х= (х 1, ..., х п) - точка n-мерного пространства; рассматривают также функции  от точек x=(x1, х2,...) нек-рого бесконечномерного пространства, к-рые, впрочем, чаще называют функционалами. Элементарные функции. Фундаментальное значение в М. а. играют элементарные функции. На практике в основном оперируют элементарными фукциями, ими приближают функции более сложной природы. Элементарные функции можно рассматривать не только для действительных, но и комплексных х;тогда представления об этих функциях становятся в определенном смысле законченными. В связи с этим возникла важная ветвь М. а., наз. теорией функций комплексного переменного, или теорией аналитических функций. Действительное число. Понятие функции существенно базируется на понятии действительного (рационального и иррационального) числа. Оно окончательно сформировалось только в конце 19 в. В частности, установлена логически безупречная связь между числами и точками геометрич. прямой, к-рая привела к формальному обоснованию идей Р. Декарта (R. Descartes, сер. 17 в.), к-рый ввел в математику прямоугольные системы координат и представление в них функций графиками. Предел. В М. а. методом изучения функций является предел. Различают предел последовательности и предел функции. Эти понятия окончательно сформировались только в 19 в., хотя представление о них имели еще др.-греч. ученые. Достаточно сказать, что Архимед (3 в. до н. э.) умел вычислять площадь сегмента параболы при помощи процесса, к-рый мы назвали бы предельным переходом (см. Исчерпывания метод). Непрерывные функции. Важный класс функций, изучаемых в М. а., образуют непрерывные функции. Одно из возможных определений этого понятия: функция y=f(x).от одного переменного х, заданная на интервале ( а, Ъ), наз. непрерывной в точке х, если  Функция непрерывна на интервале ( а, Ъ), если она непрерывна во всех его точках; тогда ее график представляет собой кривую, непрерывную в житейском понимании этого слова. Производная и дифференциал. Среди непрерывных функций следует выделить функции, имеющие производную. Производная от функции 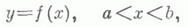 в точке хесть скорость изменения ее в этой точке, т. е. предел  Если уесть координата точки, движущейся по оси ординат в момент времени х, то f' (х).есть мгновенная скорость точки в момент времени х. По знаку производной f' (х). судят о характере изменения f(x):если f'(z)>0 (f'(x)<0). на интервале ( с, d), то функция / возрастает (убывает) на этом интервале. Если же функция / в точке хдостигает локального экстремума (максимума или минимума) и имеет в этой точке производную, то последняя равна нулю в этой точке f'(x0) = 0. Равенство (1) можно заменить эквивалентным равенством  или  где  есть линейная функция от Величина (2) наз. дифференциалом функции, соответствующим приращению  Приведенные рассуждения о дифференциале характерны для М. а. Они распространяются на функции многих переменных и на функционалы. Напр., если функция  от ппеременных имеет непрерывные частные производные в точке x=(x1, ... , xn), то ее приращение  где Здесь первый член в правой части (3) есть дифференциал dz функции f. Он линейно зависит от Пусть задан функционал (см. ст. Вариационное исчисление) 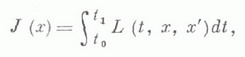 распространенный на классы В вариационном исчислении доказывается, что при известных условиях на Lприращение функционала J(х).может быть записано в виде 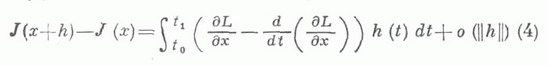 при 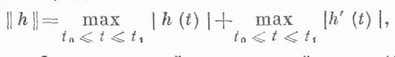 и, таким образом, второй член правой части (4) стремится к нулю быстрее, чем ||h||, а первый член линейно зависит от Интеграл. Наряду с производной интеграл имеет фундаментальное значение в М. а. Различают неопределенный и определенный интегралы. Неопределенный интеграл тесно связан с первообразной функцией. Функцию F(x).наз. первообразной от функции f на интервале ( а, b), если на этом интервале F'(x)=f(x). Определенный интеграл (Римана) от функции / на отрезке [a, b]есть предел  при 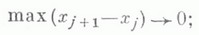 здесь   Если функция f положительна и непрерывна на отрезке [ а, b], то интеграл от нее на этом отрезке равен площади фигуры, ограниченной кривой у=f(x), осью Ох и прямыми х=а, х=b. Класс интегрируемых по Риману функций содержит все непрерывные на [ а, b]функции и нек-рые разрывные функции. Но все они необходимо ограничены. Для неограниченных функций, растущих не очень быстро, а также для нек-рых функций, заданных на бесконечных интервалах, вводят так наз. несобственные интегралы, требующие для своего определения двойного перехода к пределу. Понятие интеграла Римана для функции одного переменного распространяется на функции многих переменных (см. Кратный интеграл). С другой стороны, потребности М. а. привели к обобщению интеграла совсем в другом направлении, имеется в виду Лебега интеграл или более общий Лебега- Стилтьеса интеграл. Существенным в определении этих интегралов является введение для нек-рых множеств, называемых измеримыми, понятия их меры и на этом основании - понятия измеримой функции. Для измеримых функций и вводится интеграл Лебега - Стилтьеса. При этом рассматривается широкий диапазон разных мер и соответствующих им классов измеримых множеств и функций. Это дает возможность приспособить тот или иной интеграл к определенной конкретной задаче. Формула Ньютона - Лейбница. Между производной и интегралом имеется связь, выражаемая формулой (теоремой) Ньютона - Лейбница  Здесь f(x).непрерывная на [ а, b]функция, a F(х) - ее первообразная. Формула и ряд Тейлора. Наряду с производной и интегралом важнейшим понятием (орудием исследования) в М. а. являются Тейлора формула п Тейлора ряд. Если функция f(x), a<x<b, имеет в окрестности точки х 0 непрерывные производные до порядка пвключительно, то ее можно приблизить в этой окрестности многочленом  наз. ее многочленом Тейлора (степени п).по степеням х-x0:  (формула Тейлора); при этом ошибка приближения  стремится к нулю при 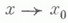 быстрее, чем   Таким образом, функция f(x).в окрестности точки х 0 может быть приближена с любой степенью точности весьма простой функцией (многочленом), требующей для своего вычисления только арифметич. операций - сложения, вычитания и умножения. Особенно важными являются так наз. аналитические в определенной окрестности х 0 функции, имеющие бесконечное число производных, такие, что для них в этой окрестности  Разложения Тейлора при определенных условиях возможны и для функций многих переменных, а также функционалов и операторов. Историческая справка. До 17 в. М. а. представлял собой совокупность решений разрозненных частных задач; напр., в интегральном исчислении - это задачи на вычисление площадей фигур, объемов тел с кривыми границами, работы переменной силы и т. д. Каждая задача или частная группа задач решалась своим методом, подчас сложным и громоздким (о предыстории М. а. см. статью Бесконечно малых исчисление), М. а. как единое и систекатич. целое сложился в трудах И. Ньютона (I. Newton), Г. Лейбница (G. Leibniz), Л. Эйлера (L. Euler), Ж. Лагранжа (J. Lagrange) и др. ученых 17 -18 вв., а его база - теория пределов - была разработана О. Коми (A. Cauchy) в нач. 19 в. Глубокий анализ исходных понятий М. а. был связан с развитием в 19-20 вв. теории множеств, теории меры, теории функций действительного переменного и привел к разнообразным обобщениям. Лит.:[1] Ла В а л л е - П у с с е н Ш.-Ж. д е, Курс анализа бесконечно малых, пер. с франц., т. 1-2, М., 1933; [2] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; 2 изд., ч. 2, М., 1980; [3] И л ь и н В. А., Садовничий В. А., Сеидов Б. X., Математический анализ, М., 1979; [4] К у д р я в ц е в Л. Д., Математический анализ, 2 изд., т. 1-2, М., 1973; [5] Никольский С. М., Курс математического анализа, 2 изд., т. 1-2, М., 1975; [6] У и т т е к е р Э. Т., В а т с о н Д ж. Н., Курс современного анализа, пер. с англ., ч. 1-2, 2 изд., М., 1962-63; [7] Ф и х т е н г о л ь ц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 1-2, М., 1970; 5 изд., т. 3, М., 1970. С. М. Никольский. |
|
|
|

 есть бесконечно малая, когда
есть бесконечно малая, когда  т. е. если функция f имеет производную в точке х, то приращение ее в этой точке разлагается на два слагаемых. Из них первое
т. е. если функция f имеет производную в точке х, то приращение ее в этой точке разлагается на два слагаемых. Из них первое  (пропорциональная
(пропорциональная 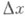 ), второе - стремится к нулю быстрее, чем
), второе - стремится к нулю быстрее, чем 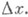
 При малых
При малых 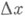 можно считать
можно считать  приближенно равным dy:
приближенно равным dy: соответствующее приращениям
соответствующее приращениям 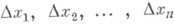 независимых переменных, можно записать в виде
независимых переменных, можно записать в виде  при
при  то есть если все
то есть если все 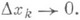

 а второй член стремится к нулю при
а второй член стремится к нулю при  быстрее, чем
быстрее, чем 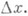
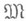 функций x(t), имеющих на отрезке [t0, t1] непрерывную производную и удовлетворяющих граничным условиям x(t0)=х 0, x(t1)=xl, где х 0, х 1 - данные числа; пусть, далее,
функций x(t), имеющих на отрезке [t0, t1] непрерывную производную и удовлетворяющих граничным условиям x(t0)=х 0, x(t1)=xl, где х 0, х 1 - данные числа; пусть, далее,  - класс функции h(t), имеющих непрерывную производную на [t0, t1] и таких, что h(t0)=h(t1)=0. Очевидно, если
- класс функции h(t), имеющих непрерывную производную на [t0, t1] и таких, что h(t0)=h(t1)=0. Очевидно, если 
 где
где 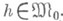 Первый член в (4) наз. вариацией функционала и обозначается dJ(x, h).
Первый член в (4) наз. вариацией функционала и обозначается dJ(x, h). при
при  они могут быть представлены в виде бесконечного степенного ряда Тейлора:
они могут быть представлены в виде бесконечного степенного ряда Тейлора: