"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА
Значение МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА в математической энциклопедии:
с отказами - система массового обслуживания, алгоритм к-рой предусматривает выбывание вызовов, в момент прихода к-рых все каналы оказались занятыми. Основные определения и обозначения см. в ст. Массового обслуживания система.
1) Естественными характеристиками состояния М. о. с. с отказами являются число qn (или q(t)).занятых линий в момент прихода п-го вызова (в момент времени t). Однако, в отличие от систем с бесконечным числом каналов обслуживания, здесь всегда  где т - число каналов в системе. Если в момент прихода n-го вызова оказывается q п=т, то этот вызов получает отказ и выбывает из рассмотрения. Если же q п<m, то вызов направляется на обслуживание в один из свободных каналов.
где т - число каналов в системе. Если в момент прихода n-го вызова оказывается q п=т, то этот вызов получает отказ и выбывает из рассмотрения. Если же q п<m, то вызов направляется на обслуживание в один из свободных каналов.
Предположив, что управляющая последовательность  метрически транзитивна,
метрически транзитивна,  можно сформулировать эргодич. теорему для систем с отказами, используя систему с бесконечным числом каналов обслуживания, управляемую той же последовательностью. Для такой системы существует собственная стационарная последовательность {Qk} длины очереди. Величину Q0 можно представлять как число занятых линий стационарной системы в момент прихода нек-рого вызова. Обозначив условно номер этого вызова через g, определяют
можно сформулировать эргодич. теорему для систем с отказами, используя систему с бесконечным числом каналов обслуживания, управляемую той же последовательностью. Для такой системы существует собственная стационарная последовательность {Qk} длины очереди. Величину Q0 можно представлять как число занятых линий стационарной системы в момент прихода нек-рого вызова. Обозначив условно номер этого вызова через g, определяют  как число линий, занятых вызовами, пришедшими до вызова g0, в момент прихода вызова с номером g+l, так что
как число линий, занятых вызовами, пришедшими до вызова g0, в момент прихода вызова с номером g+l, так что  Тогда если вероятность события
Тогда если вероятность события

положительна, то распределения последовательностей  длин очереди для систем с отказами будут сходиться при
длин очереди для систем с отказами будут сходиться при  к распределению нек-рой стационарной последовательности
к распределению нек-рой стационарной последовательности 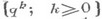 . Смысл события Авесьма прост: оно состоит в "обновлении" системы: после него в системе будут находиться лишь вызовы с номерами уи выше.
. Смысл события Авесьма прост: оно состоит в "обновлении" системы: после него в системе будут находиться лишь вызовы с номерами уи выше.
Приведенная теорема есть частный случай более общего утверждения, использующего т. н. метод обновлений. Если  то для выполнения сформулированных условий достаточно, чтобы
то для выполнения сформулированных условий достаточно, чтобы

Утверждение, аналогичное сформулированному выше, будет иметь место и относительно сходимости при  процессов
процессов  к стационарному процессу
к стационарному процессу  длины очереди. При этом помимо приведенных условий дополнительно требуется, чтобы входной процесс е(t).(число поступивших вызовов к моменту времени t).был процессом со стационарными приращениями.
длины очереди. При этом помимо приведенных условий дополнительно требуется, чтобы входной процесс е(t).(число поступивших вызовов к моменту времени t).был процессом со стационарными приращениями.
2) Если  то справедливы формулы Э р л а н г а
то справедливы формулы Э р л а н г а

где

a - показатель распределения

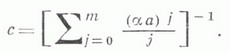
Если 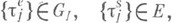 то последовательность q п связана в простую однородную цепь Маркова с конечным числом (m+1) состояний. В этом случае вероятности
то последовательность q п связана в простую однородную цепь Маркова с конечным числом (m+1) состояний. В этом случае вероятности
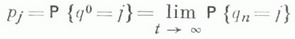
также можно найти в явном виде. Если, кроме того, распределение 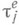 нерешетчато и
нерешетчато и 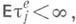 то
то

где a - показатель распределения
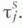
Эти утверждения указывают условия существования и явный вид для стационарной вероятности отказа, равной
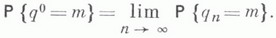
3) Теоремы устойчивости для систем с отказами вполне аналогичны теоремам устойчивости для систем с бесконечным числом каналов. Пусть даны последовательности 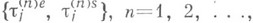 управляющие системами с отказами и удовлетворяющие следующему условию:
управляющие системами с отказами и удовлетворяющие следующему условию:
(А) существует последовательность 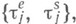 к распределениям к-рой сходятся при
к распределениям к-рой сходятся при  конечномерные распределения
конечномерные распределения  Кроме того, все названные последовательности удовлетворяют условиям (см., напр., п. 1), обеспечивающим существование стационарных последовательностей длины очереди. Чтобы имела место сходимость распределений этих стационарных последовательностей длины очереди, к-рые обозначены
Кроме того, все названные последовательности удовлетворяют условиям (см., напр., п. 1), обеспечивающим существование стационарных последовательностей длины очереди. Чтобы имела место сходимость распределений этих стационарных последовательностей длины очереди, к-рые обозначены 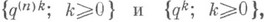 следует ввести еще два условия:
следует ввести еще два условия:
(В) 
(С).распределения
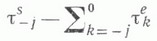
при всех  непрерывны в точке 0.
непрерывны в точке 0.
При выполнении условий (А), (В), (С) конечномерные распределения последовательности  слабо сходятся к распределениям
слабо сходятся к распределениям 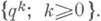
4) Асимптотич. методы исследования систем с отказами могут быть эффективными также при изучении систем с интенсивным входным потоком или с большим числом каналов обслуживания.
Исследование систем с интенсивным входом связано с получением результатов в предположениях, близких к тем, к-рые рассматриваются при асимптотич. анализе систем с бесконечным числом каналов обслуживания. Изучение систем с большим числом каналов проводится как путем асимптотич. анализа явных формул, к-рые становятся малоэффективными при больших m, так и с помощью изучения близости распределения qk к распределению числа занятых линий в аналогичной системе, но с бесконечным числом каналов обслуживания.
Напр., для систем с последовательностями 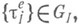
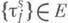 стационарная вероятность отказа равна
стационарная вероятность отказа равна

где
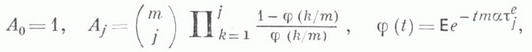
a - показатель распределения 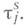 Эти соотношения при больших тстановятся малопригодными для отыскания числовых значений р т. В то же время оказывается, что при
Эти соотношения при больших тстановятся малопригодными для отыскания числовых значений р т. В то же время оказывается, что при  действуют достаточно простые формулы, к-рые устанавливают асимптотич. поведение р т и к-рые, следовательно, можно использовать для приближенных вычислений вероятности отказа. При этом определяющую роль играет параметр
действуют достаточно простые формулы, к-рые устанавливают асимптотич. поведение р т и к-рые, следовательно, можно использовать для приближенных вычислений вероятности отказа. При этом определяющую роль играет параметр 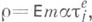 характеризующий отношение среднего числа
характеризующий отношение среднего числа 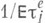 вызовов, поступивших в систему, к среднему числу вызовов
вызовов, поступивших в систему, к среднему числу вызовов  к-рое может обслужить система за единицу времени. Если r<1, то система обычно полностью загружена, если r>1, то система недогружена. Если r<1-e при
к-рое может обслужить система за единицу времени. Если r<1, то система обычно полностью загружена, если r>1, то система недогружена. Если r<1-e при  и нек-ром e>0, то
и нек-ром e>0, то 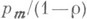
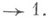 Если
Если 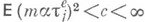 при
при  то приведенное соотношение для р т сохраняется и при
то приведенное соотношение для р т сохраняется и при 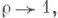 если только
если только 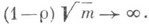 Если же
Если же 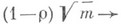
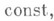 то р т ведет себя асимптотически как
то р т ведет себя асимптотически как 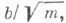 где постоянная bнайдена в явном виде. Найдено также асимптотич. поведение р т и в случае
где постоянная bнайдена в явном виде. Найдено также асимптотич. поведение р т и в случае 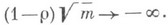
5) Несколько более полно могут быть изучены одно-канальные системы с отказами (когда m=1). Пусть, напр.,  Случайную величину h) определяют равенством
Случайную величину h) определяют равенством
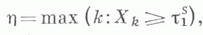
где  Тогда, для того чтобы при любом начальном условии существовал предел
Тогда, для того чтобы при любом начальном условии существовал предел
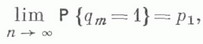
необходимо и достаточно, чтобы наибольший общий делитель возможных значений h равнялся 1. При этом  Если t е нерешетчата, то всегда существует
Если t е нерешетчата, то всегда существует

При более широком понимании вероятности отказа как предела отношения p=rn/n, где rn - число необслуженных вызовов среди первых n поступивших, условия существования lim pn будут более широкими. Напр., для случая 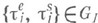 предел pn существует всегда и равен
предел pn существует всегда и равен 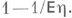
Лит. см. при ст. Массового обслуживания теория.
А. А. Боровков.





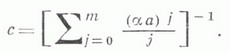
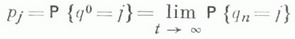

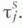
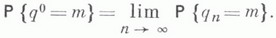
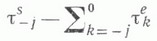

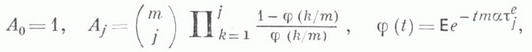
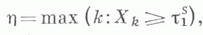
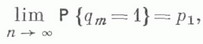


 где т - число каналов в системе. Если в момент прихода n-го вызова оказывается q п=т, то этот вызов получает отказ и выбывает из рассмотрения. Если же q п<m, то вызов направляется на обслуживание в один из свободных каналов.
где т - число каналов в системе. Если в момент прихода n-го вызова оказывается q п=т, то этот вызов получает отказ и выбывает из рассмотрения. Если же q п<m, то вызов направляется на обслуживание в один из свободных каналов. метрически транзитивна,
метрически транзитивна,  можно сформулировать эргодич. теорему для систем с отказами, используя систему с бесконечным числом каналов обслуживания, управляемую той же последовательностью. Для такой системы существует собственная стационарная последовательность {Qk} длины очереди. Величину Q0 можно представлять как число занятых линий стационарной системы в момент прихода нек-рого вызова. Обозначив условно номер этого вызова через g, определяют
можно сформулировать эргодич. теорему для систем с отказами, используя систему с бесконечным числом каналов обслуживания, управляемую той же последовательностью. Для такой системы существует собственная стационарная последовательность {Qk} длины очереди. Величину Q0 можно представлять как число занятых линий стационарной системы в момент прихода нек-рого вызова. Обозначив условно номер этого вызова через g, определяют  как число линий, занятых вызовами, пришедшими до вызова g0, в момент прихода вызова с номером g+l, так что
как число линий, занятых вызовами, пришедшими до вызова g0, в момент прихода вызова с номером g+l, так что  Тогда если вероятность события
Тогда если вероятность события  длин очереди для систем с отказами будут сходиться при
длин очереди для систем с отказами будут сходиться при  к распределению нек-рой стационарной последовательности
к распределению нек-рой стационарной последовательности 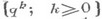 . Смысл события Авесьма прост: оно состоит в "обновлении" системы: после него в системе будут находиться лишь вызовы с номерами уи выше.
. Смысл события Авесьма прост: оно состоит в "обновлении" системы: после него в системе будут находиться лишь вызовы с номерами уи выше. то для выполнения сформулированных условий достаточно, чтобы
то для выполнения сформулированных условий достаточно, чтобы  процессов
процессов  к стационарному процессу
к стационарному процессу  длины очереди. При этом помимо приведенных условий дополнительно требуется, чтобы входной процесс е(t).(число поступивших вызовов к моменту времени t).был процессом со стационарными приращениями.
длины очереди. При этом помимо приведенных условий дополнительно требуется, чтобы входной процесс е(t).(число поступивших вызовов к моменту времени t).был процессом со стационарными приращениями. то справедливы формулы Э р л а н г а
то справедливы формулы Э р л а н г а 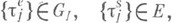 то последовательность q п связана в простую однородную цепь Маркова с конечным числом (m+1) состояний. В этом случае вероятности
то последовательность q п связана в простую однородную цепь Маркова с конечным числом (m+1) состояний. В этом случае вероятности 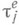 нерешетчато и
нерешетчато и 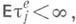 то
то 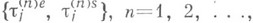 управляющие системами с отказами и удовлетворяющие следующему условию:
управляющие системами с отказами и удовлетворяющие следующему условию: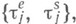 к распределениям к-рой сходятся при
к распределениям к-рой сходятся при  конечномерные распределения
конечномерные распределения  Кроме того, все названные последовательности удовлетворяют условиям (см., напр., п. 1), обеспечивающим существование стационарных последовательностей длины очереди. Чтобы имела место сходимость распределений этих стационарных последовательностей длины очереди, к-рые обозначены
Кроме того, все названные последовательности удовлетворяют условиям (см., напр., п. 1), обеспечивающим существование стационарных последовательностей длины очереди. Чтобы имела место сходимость распределений этих стационарных последовательностей длины очереди, к-рые обозначены 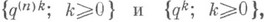 следует ввести еще два условия:
следует ввести еще два условия:
 непрерывны в точке 0.
непрерывны в точке 0. слабо сходятся к распределениям
слабо сходятся к распределениям 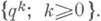
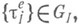
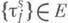 стационарная вероятность отказа равна
стационарная вероятность отказа равна 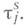 Эти соотношения при больших тстановятся малопригодными для отыскания числовых значений р т. В то же время оказывается, что при
Эти соотношения при больших тстановятся малопригодными для отыскания числовых значений р т. В то же время оказывается, что при  действуют достаточно простые формулы, к-рые устанавливают асимптотич. поведение р т и к-рые, следовательно, можно использовать для приближенных вычислений вероятности отказа. При этом определяющую роль играет параметр
действуют достаточно простые формулы, к-рые устанавливают асимптотич. поведение р т и к-рые, следовательно, можно использовать для приближенных вычислений вероятности отказа. При этом определяющую роль играет параметр 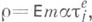 характеризующий отношение среднего числа
характеризующий отношение среднего числа 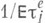 вызовов, поступивших в систему, к среднему числу вызовов
вызовов, поступивших в систему, к среднему числу вызовов  к-рое может обслужить система за единицу времени. Если r<1, то система обычно полностью загружена, если r>1, то система недогружена. Если r<1-e при
к-рое может обслужить система за единицу времени. Если r<1, то система обычно полностью загружена, если r>1, то система недогружена. Если r<1-e при  и нек-ром e>0, то
и нек-ром e>0, то 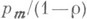
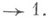 Если
Если 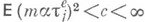 при
при  то приведенное соотношение для р т сохраняется и при
то приведенное соотношение для р т сохраняется и при 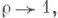 если только
если только 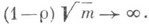 Если же
Если же 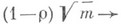
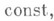 то р т ведет себя асимптотически как
то р т ведет себя асимптотически как 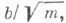 где постоянная bнайдена в явном виде. Найдено также асимптотич. поведение р т и в случае
где постоянная bнайдена в явном виде. Найдено также асимптотич. поведение р т и в случае 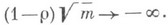
 Случайную величину h) определяют равенством
Случайную величину h) определяют равенством  Тогда, для того чтобы при любом начальном условии существовал предел
Тогда, для того чтобы при любом начальном условии существовал предел  Если t е нерешетчата, то всегда существует
Если t е нерешетчата, то всегда существует 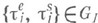 предел pn существует всегда и равен
предел pn существует всегда и равен