|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМАЗначение МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА в математической энциклопедии: с ожиданием многоканальная - система массового обслуживания, алгоритм к-рой предусматривает накапливание вызовов в очереди, если в момент их прихода система оказалась занятой; при этом обслуживание вызовов ведется в нескольких каналах одновременно. Основные определения и обозначения см. в ст. Массового обслуживания система. Функционирование многоканальных систем с очередью, управляемых последовательностью 1) Для наглядности изложения использованы следующие обозначения: а вектор 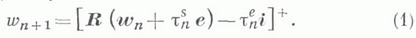 Если последовательность Если  Если  то  Здесь все случайные величины, стоящие под знаком вероятности, независимы. Если, кроме того, распределение  2) Если  описываются как известного вида рациональные функции от значений m, и  Если k>m, то  причем Аот k не зависит. Для предельного распределения времени ожидания  имеет место равенство 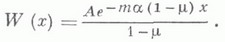 Если 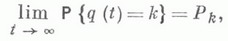 где 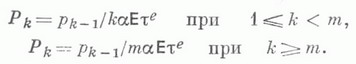 В случае
где  3) Теоремы устойчивости (о непрерывной зависимости стационарного распределения 4) Асимптотич. методы исследования многоканальных систем для больших нагрузок дают результаты, аналогичные соответствующим результатам для одно-канальных систем. Пусть в схеме серий для управляющих последовательностей . (wDd равно разности между средним количеством вызовов, поступивших в систему, и средним количеством вызовов, к-рое система может обслужить за единицу времени; если  и при   где w(u).- стандартный винеровский процесс; при   при   Аналогичные соотношения верны для длины qn очереди и для времени Другое возможное направление асимптотич. исследований для многоканальных систем состоит в изучении систем с интенсивным входным потоком и неограниченно возрастающим (вместе с 5) Поведение многоканальных систем с бесконечным числом каналов обслуживания, управляемых последовательностью Пусть  где I{А} индикатор события А. Условие 6) Для систем, у к-рых  Число q0 (х).указывает, сколько вызовов осталось в системе, работающей в стационарном режиме, спустя время хпосле прихода нек-рого вызова, но без учета данного вызова и всех вызовов, поступающих после него. Обозначив  получают  система функций Pj(x)удовлетворяет уравнениям  Здесь Р -1 (х).следует положить, равной 0. Каждые из первых k+1 уравнений этой системы относительно  Аналогичные утверждения справедливы для распределения процесса q(t). Если  то  где  a - показатель распределения  Если  то  где  a - показатель распределения  7) Теоремы устойчивости в случае Для схемы серий, когда система управляется стационарными последовательностями (А) Существует последовательность  такая, что (В) (С) Распределения непрерывны в точке 0. Теорема устойчивости утверждает тогда, что при выполнении условий (А), (В), (С) распределения последовательностей {q(n)k} длин очередей (к-рые определяются равенством (2) с управляющими последовательностями Все три условия (А), (В), (С), присутствующие в этом утверждении, существенны; отказ хотя бы от одного из них сразу позволяет строить примеры, где сходимость распределений {q(n)k} отсутствует. 8) Асимптотич. анализ систем с бесконечным числом каналов обслуживания становится естественным и эффективным при изучении т. н. нагруженных систем, когда велика интенсивность входного потока. Несомненным преимуществом асимптотич. подхода является большая общность и универсальность установленных закономерностей. Пусть входной поток  слабо сходятся при Если, напр.,  x(t).- стандартный винеровский процесс. Относительно обслуживающего устройства предполагают, что 1) Если  слабо сходятся при  2) Если  слабо сходятся к конечномерным распределениям процесса  где q(t) -центрированный гауссовский процесс, не зависящий от x(t), с ковариационной функцией  Если потребовать от функций m(t).пли G(t).нек-рой гладкости, то сходимость процессов zi(t).к процессам zi(t), i=1, 2, будет иметь место и в более сильном смысле (напр., сходимость распределений f(zi(t)) к Лит. см. при ст. Массового обслуживания теория. А. А. Боровков. |
|
|
|

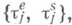 происходит следующим образом. Вызовы прибывают в моменты времени
происходит следующим образом. Вызовы прибывают в моменты времени 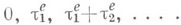 На обслуживание вызова с номером j тратится время
На обслуживание вызова с номером j тратится время 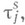 в каком бы из
в каком бы из 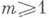 каналов ни обслуживался этот вызов. Пришедшие вызовы тут же направляются (в порядке поступления) в любой свободный канал, если каналы не все заняты, или ждут, когда освободится какой-нибудь из каналов, куда и поступают на обслуживание. Пусть для простоты в момент времени t=0 система свободна.
каналов ни обслуживался этот вызов. Пришедшие вызовы тут же направляются (в порядке поступления) в любой свободный канал, если каналы не все заняты, или ждут, когда освободится какой-нибудь из каналов, куда и поступают на обслуживание. Пусть для простоты в момент времени t=0 система свободна.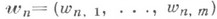 - вектор времени ожидания n-го вызова, где wn,j - время, к-рое должен ждать этот вызов до освобождения i каналов от вызовов, пришедших раньше, чем он; так что wn,1 - "истинное" время ожидания. Пусть, кроме того,
- вектор времени ожидания n-го вызова, где wn,j - время, к-рое должен ждать этот вызов до освобождения i каналов от вызовов, пришедших раньше, чем он; так что wn,1 - "истинное" время ожидания. Пусть, кроме того,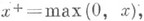
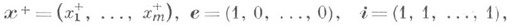
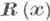 получен из
получен из 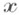 упорядочиванием по возрастанию его координат (так что первая координата
упорядочиванием по возрастанию его координат (так что первая координата 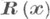 равна min(x1, . . ., х т)).Тогда имеет место следующее рекуррентное соотношение для
равна min(x1, . . ., х т)).Тогда имеет место следующее рекуррентное соотношение для 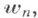 обобщающее свой одномерный аналог
обобщающее свой одномерный аналог 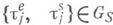 и
и 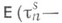
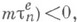 то существует собственная последовательность
то существует собственная последовательность  удовлетворяющая (1) и такая, что функция распределения
удовлетворяющая (1) и такая, что функция распределения  при
при  монотонно сходится к функции распределения
монотонно сходится к функции распределения 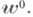 Это утверждение допускает обобщение на случай
Это утверждение допускает обобщение на случай 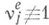 и распространяется также на длину qn очереди в момент прихода n-го вызова (под qn понимают очередь, включая вызовы, находящиеся на обслуживании). Существуют формулы, связывающие предельные распределения для
и распространяется также на длину qn очереди в момент прихода n-го вызова (под qn понимают очередь, включая вызовы, находящиеся на обслуживании). Существуют формулы, связывающие предельные распределения для  и qn.
и qn. то (1) позволяет записать интегральное уравнение для стационарного распределения w0. В этом случае можно указать также простые связи между стационарными распределениями длины очереди и времени ожидания. Именно, если
то (1) позволяет записать интегральное уравнение для стационарного распределения w0. В этом случае можно указать также простые связи между стационарными распределениями длины очереди и времени ожидания. Именно, если  означает k-ю координату вектора
означает k-ю координату вектора  то при
то при  существуют
существуют  нерешетчато, то аналогичные формулы верны и для предельного распределения q(t). Если
нерешетчато, то аналогичные формулы верны и для предельного распределения q(t). Если  то
то  то можно указать явные формулы для предельных распределений qn, q(t),
то можно указать явные формулы для предельных распределений qn, q(t), Пусть а - показатель распределения
Пусть а - показатель распределения  и
и  Тогда числа
Тогда числа  где m - единственный корень в области |m|<1 уравнения
где m - единственный корень в области |m|<1 уравнения  - нерешетчатая случайная величина, то существуют
- нерешетчатая случайная величина, то существуют 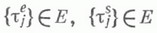

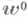 от распределений
от распределений  и
и 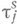 ) получены в менее общей форме, чем для одноканальных систем, и связаны с условием о существовании т. н. обновляющих событий. Однако в случае
) получены в менее общей форме, чем для одноканальных систем, и связаны с условием о существовании т. н. обновляющих событий. Однако в случае  это условие с необходимостью выполнено. Если для таких систем в схеме серий распределения
это условие с необходимостью выполнено. Если для таких систем в схеме серий распределения  слабо сходятся соответственно к распределениям
слабо сходятся соответственно к распределениям  и, кроме того,
и, кроме того,  то распределение
то распределение  будет слабо сходится к распределению
будет слабо сходится к распределению 
 выполнено условие
выполнено условие 
 то в качестве параметра б можно выбрать число
то в качестве параметра б можно выбрать число  имеющее тот же смысл). Тогда если
имеющее тот же смысл). Тогда если  равномерно ограничены при нек-ром e>0, то для длины q(t).очереди в момент времени tсправедливы при
равномерно ограничены при нек-ром e>0, то для длины q(t).очереди в момент времени tсправедливы при  следующие соотношения:
следующие соотношения: ожидания.
ожидания. ) числом каналов обслуживания.
) числом каналов обслуживания. описывается так же, как поведение многоканальных систем с очередью, с той лишь разницей, что здесь всегда есть свободные каналы и, следовательно, время ожидания для любого вызова равно 0. В качестве характеристики состояния системы рассматривают число qn занятых линий в момент прихода n-го вызова или число q(t).занятых линий в момент времени t(как и везде выше qn и q(t).- длины очереди и q1=0).
описывается так же, как поведение многоканальных систем с очередью, с той лишь разницей, что здесь всегда есть свободные каналы и, следовательно, время ожидания для любого вызова равно 0. В качестве характеристики состояния системы рассматривают число qn занятых линий в момент прихода n-го вызова или число q(t).занятых линий в момент времени t(как и везде выше qn и q(t).- длины очереди и q1=0). и, кроме того, последовательность
и, кроме того, последовательность  метрически транзитивна. Тогда если
метрически транзитивна. Тогда если  <
<  то распределение последовательности
то распределение последовательности 
 при
при  монотонно сходится к распределению собственной стационарной последовательности
монотонно сходится к распределению собственной стационарной последовательности  близко к необходимому условию для конечности (2).
близко к необходимому условию для конечности (2). распределение стационарной длины qk очереди можно описать с помощью уравнений. Для этого следует ввести, величины
распределение стационарной длины qk очереди можно описать с помощью уравнений. Для этого следует ввести, величины  имеют единственное решение в классе функций ограниченной вариации, обладающих свойствами
имеют единственное решение в классе функций ограниченной вариации, обладающих свойствами  Если, кроме того,
Если, кроме того,  - нерешетчатые случайные величины, то
- нерешетчатые случайные величины, то  как и в предыдущих разделах, выясняют условия, при к-рых малое изменение управляющих последовательностей влечет за собой малое изменение стационарного распределения числа qk занятых линий.
как и в предыдущих разделах, выясняют условия, при к-рых малое изменение управляющих последовательностей влечет за собой малое изменение стационарного распределения числа qk занятых линий. зависящими от параметра n=1, 2, . . ., пусть выполнены следующие условия.
зависящими от параметра n=1, 2, . . ., пусть выполнены следующие условия. метрически транзитивна,
метрически транзитивна, и конечномерные распределения
и конечномерные распределения  сходятся при
сходятся при  к распределениям
к распределениям 
 при
при 
 при всех
при всех 
 ) сходятся при
) сходятся при  к распределениям {qk}.
к распределениям {qk}. означающий число вызовов, поступавших в систему к моменту времени t, зависит от параметра
означающий число вызовов, поступавших в систему к моменту времени t, зависит от параметра  (схема серий), так что
(схема серий), так что  при
при  для каждого фиксированного t>0, и, кроме того, существуют неубывающая функция m(t), функция
для каждого фиксированного t>0, и, кроме того, существуют неубывающая функция m(t), функция  при
при  и непрерывный случайный процесс x(t), заданный на [0, t0], такие, что распределения
и непрерывный случайный процесс x(t), заданный на [0, t0], такие, что распределения  где
где  к распределению
к распределению  для любого измеримого и непрерывного относительно равномерной метрики функционала f.
для любого измеримого и непрерывного относительно равномерной метрики функционала f. и управление системой происходит с помощью последовательности
и управление системой происходит с помощью последовательности  то сформулированные условия будут выполнены при любом t0, при этом
то сформулированные условия будут выполнены при любом t0, при этом  Тогда:
Тогда: то конечномерные распределения нормированного процесса очереди
то конечномерные распределения нормированного процесса очереди  к распределениям процесса
к распределениям процесса  то конечномерные распределения процесса
то конечномерные распределения процесса  при
при  для всех функционалов, непрерывных относительно равномерной метрики).
для всех функционалов, непрерывных относительно равномерной метрики).