|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМАЗначение МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА в математической энциклопедии: с ожиданнем и одним каналом обслуживания - система массового обслуживания, алгоритм к-рой предусматривает, что вызовы, не принятые немедленно к обслуживанию (заставшие систему занятой), накапливаются в очереди; при этом обслуживание следующего вызова (или партии вызовов) может начаться лишь после того, как окончится обслуживание предыдущего (или предыдущей партии, если вызовы обслуживаются группами). Основные определения и обозначения см. в ст. Массового обслуживания система. Наиболее естественными характеристиками состояния систем с очередью являются следующие: а) время wn ожидания начала обслуживания требования с номером пи виртуальное время w(t).ожидания, к-рое определяется как время, необходимое для освобождения системы от вызовов, пришедших до момента времени t; б) длина q п очереди в момент прихода n-го вызова и длина q(t).очереди в момент времени t. 1) В "ординарном" случае  Такого же типа уравнениями (для времени ожидания или для длины очереди) могут описываться системы с ожиданием и в "неординарном" случае, когда  где bn - число вызовов, к-рое может быть обслужено за время 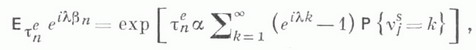 где а - показатель распределения Если обозначить 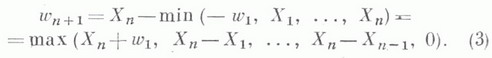 Отсюда следует, что если при любом фиксированном интервале 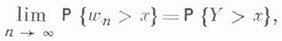 где 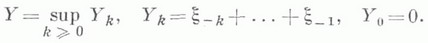 Здесь величины 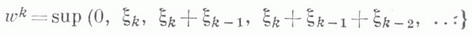 удовлетворяют уравнению (1) и имеют распределение, совпадающее с предельным распределением wn. Это - стационарный процесс времени ожидания. Пусть последовательность 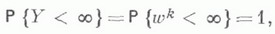 если если 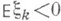 или если или если 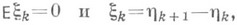 где где  В остальных случаях В остальных случаях 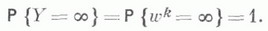 Если 2) Как уже отмечалось, другой возможной характеристикой состояния системы является виртуальное время w(t).ожидания. Грубо говоря, это - время, к-рое прождал бы начала своего обслуживания вызов, пришедший в момент t. Пусть S(t) есть сумма времен обслуживания вызовов, поступивших в систему до момента времени t, X(t)=S(t)-t. Аналогом равенства (3) здесь является соотношение 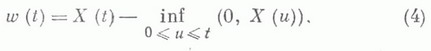 Пусть GIS- класс процессов со стационарными в узком смысле приращениями и GII - класс процессов с независимыми приращениями (GII и GIS здесь можно понимать и более узко; напр., можно считать, что GII - класс обобщенных пуассоновских процессов с положительными скачками и сносом -1). Если процесс  где 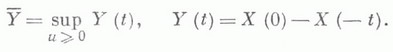 Если, кроме того, 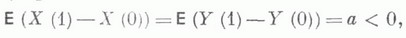 то распределение процесса 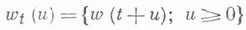 сходится при 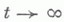 к распределению процесса 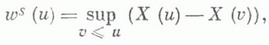 к-рый является собственным стационарным процессом виртуального времени ожидания. Сходимость здесь имеет место в сильной форме: 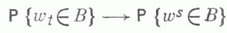 для любого измеримого В. Далее, если 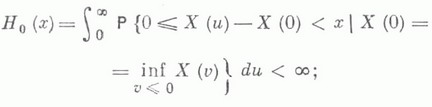 при этом 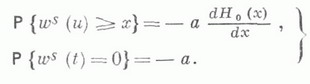 Приведенные формулы сохраняются и в случае Для систем, у к-рых  Если же 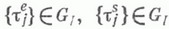 и распределение 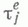 нерешетчато, то существует 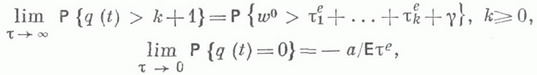 где все компоненты под знаком вероятности в правой части независимы, g имеет плотность, равную 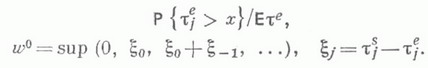 Если 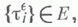 то предельные распределения qn и q(t).совпадают. 4) Если  (допускается также, что 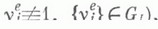 то можно получить точные формулы и для допредельного распределения w(t). 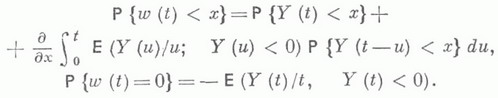 При a<0 и 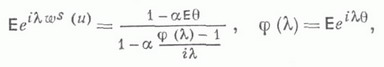 где q - величина скачка процесса X(t)( 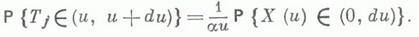 5) Для систем, у к-рых 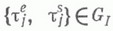 (допускается, также распределение wk совпадает с распределением величины 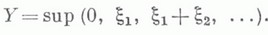 По известному распределению xj распределение Yможет быть найдено следующим образом. Если 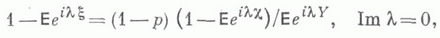 где 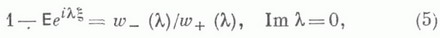 в к-ром функции 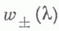 допускают представление 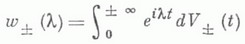 ( Предполагают, что 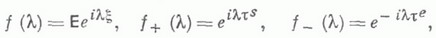 так что А) Если венно, то функция (1-f)Qn в области Iml<0 имеет ровно пнулей l1, ..., ln и 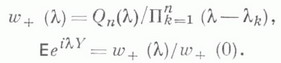 Это означает, что если распределение ts представимо в виде 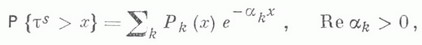 где Р k (х) - многочлены, то такого же вида представление (при других ak и Р k, определяемых нулями l1, ..., ln) будет иметь место и для В) Если 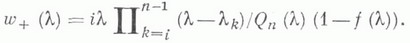 Кроме этих формул, дающих явное выражение для распределения У, можно также в широком классе случаев описать асимптотич. поведение 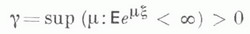 и 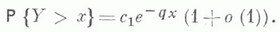 Если же 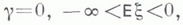 то 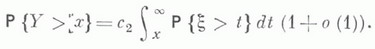 Постоянные с 1 и с 2 найдены в явном виде. Результаты, аналогичные изложенным в пп. 2) - 5), справедливы и для систем с дискретным временем, когда время tи случайные величины управляющих последовательностей принимают лишь целочисленные значения. 6) Теоремы устойчивости выясняют условия, при к-рых малое изменение конечномерных распределений управляющих последовательностей влечет за собой малое изменение стационарного распределения времени ожидания или длины очереди. Важность вопроса об устойчивости систем обслуживания объясняется тем, что обычно в реальных задачах пользуются теми или иными предположениями о природе управляющей последовательности (напр., предполагается, что xj независимы или что tej распределены по показательному закону), в то время как на самом деле эти предположения выполняются лишь приближенно. Спрашивается, будет ли решение таких "идеализированных" задач близко к решению истинной задачи. Чтобы получить точную постановку проблемы рассматривают схему серий, когда уравнением (1) управляют стационарные последовательности (серия последовательностей) 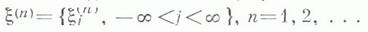 Кроме того, рассматривают стационарную последовательность  и обозначают 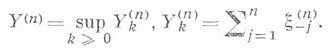 Ответ на поставленный выше вопрос дает следующее утверждение. Пусть конечномерные распределения x(n) слабо сходятся к соответствующим распределениям последовательности x, относительно к-рой предполагается, что она эргодична и 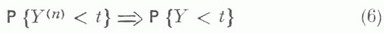 (т. е. для сходимости распределений стационарных времен ожидания) достаточно, чтобы 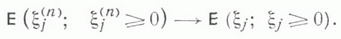 Сформулированное условие сходимости близко к необходимому. Если управляющие последовательности 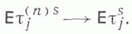 Аналогично обстоит дело со стационарным распределением виртуального времени ws(t).ожидания. Если конечномерные распределения процессов 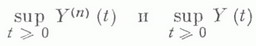 достаточно, чтобы 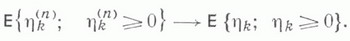 7) Асимптотич. методы исследования одноканалъных систем (они включают в себя и теоремы устойчивости) дают приближенные формулы для случая больших и малых нагрузок. Пусть 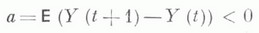 близко к 0, и малую нагрузку, если аблизко к -1. Точная постановка задачи связана здесь как и в п. 6) с введением схемы серий. Именно, для случая больших нагрузок рассматривают процессы Xa(t), зависящие от параметра  равномерно по а, где 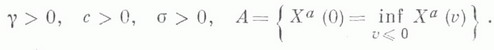 Тогда для стационарного виртуального времени ws(t).при 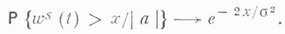 Аналогичный результат будет иметь место и для стационарного распределения wk. Если условия большой нагрузки наложить на последовательности 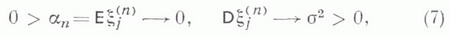 то весьма полно можно описать также и распределение допредельного времени wn ожидания, включая т. н. переходные явления. Именно, пусть в дополнение к (7) 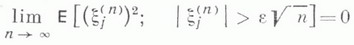 при любом 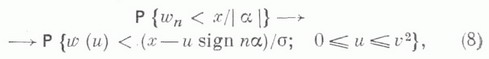 где w(и) - стандартный винеровскии процесс. Значение правой части (8) вычислено в явном виде. Если 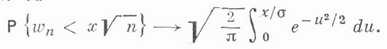 Если 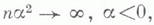 то 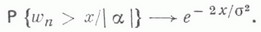 Если 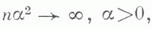 то 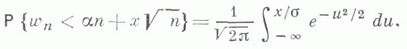 8) Системы с ограниченной очередью характеризуются тем, что вызовы, пришедшие в систему и заставшие очередь объема Уравнения (2) здесь следует заменить на уравнение вида 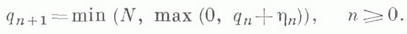 Пусть Если, кроме того, Существует также следующее представление для стационарного паспведеления: 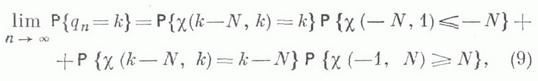 где 9) В системах с автономным обслуживанием обслуживание вызовов в отличие от обычных систем с ожиданием может начинаться лишь в моменты времени О, Наряду с процессом {e(t)}, описывающим входящий поток, рассматривают процесс {s(t)}, где s(t).определяется как число вызовов, к-рое приняла бы на обслуживание система к моменту tпри бесконечной очереди. Обозначив через q(t).длину очереди в момент t, не считая вызовов уже находящихся на обслуживании, и положив X(t) = e(t)-s(t), получают 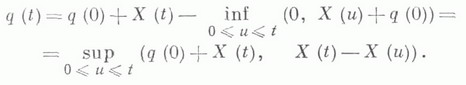 Это равенство аналогично соотношению (4) и приводит к следующему результату. Если процесс 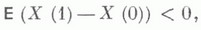 то распределение процессов то распределение процессов 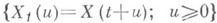 сходится при 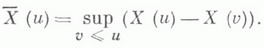 Если Лит. см. при ст. Массового обслуживания теория. А. А. Боровков. |
|
|
|

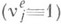 значения wn связаны рекуррентным соотношением
значения wn связаны рекуррентным соотношением 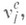
 отличны от единицы. Напр., для длины qn очереди справедливы соотношения
отличны от единицы. Напр., для длины qn очереди справедливы соотношения  при бесперебойной работе системы. Если
при бесперебойной работе системы. Если 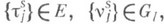 то распределение bn можно найти из соотношений
то распределение bn можно найти из соотношений 
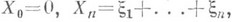 то решение уравнения (1) имеет вид
то решение уравнения (1) имеет вид 
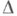 и
и 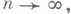 то существует предельное распределение времени ожидания:
то существует предельное распределение времени ожидания: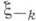 - элементы последовательности
- элементы последовательности 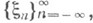 являющейся расширением
являющейся расширением 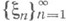 до последовательности, стационарной на всей оси. В дальнейшем будет предполагаться что такое расширение произведено над всеми управляющими последовательностями. Значения
до последовательности, стационарной на всей оси. В дальнейшем будет предполагаться что такое расширение произведено над всеми управляющими последовательностями. Значения 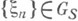 и эргодична (
и эргодична (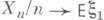 с вероятностью 1). Тогда
с вероятностью 1). Тогда 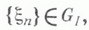 то
то 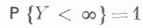 тогда и только тогда, когда
тогда и только тогда, когда 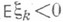 (тривиальный случай
(тривиальный случай 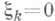 исключается).
исключается).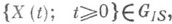 то он может быть расширен до процесса
то он может быть расширен до процесса 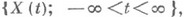 заданного на всей оси и также принадлежащего GIS В этом случае существует
заданного на всей оси и также принадлежащего GIS В этом случае существует 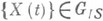 и а<0, то существует условная функция восстановления Н 0 (х).процесса X(t).
и а<0, то существует условная функция восстановления Н 0 (х).процесса X(t).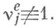
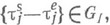 существуют простые связи между распределениями wk и ws(t).3) Эргодические теоремы для длины очереди могут быть получены с помощью соответствующих теорем для времени ожидания. Пусть, напр., последовательность
существуют простые связи между распределениями wk и ws(t).3) Эргодические теоремы для длины очереди могут быть получены с помощью соответствующих теорем для времени ожидания. Пусть, напр., последовательность 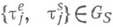 эргодична (метрически транзи-тивна).' Если, кроме того,
эргодична (метрически транзи-тивна).' Если, кроме того, 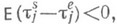 то существует предельное (стационарное) распределение qn такое, что
то существует предельное (стационарное) распределение qn такое, что  имеет место формула X и н ч и н а для стационарного распределения:
имеет место формула X и н ч и н а для стационарного распределения: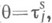 если
если 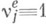 ), a - показатель распределения
), a - показатель распределения 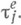 Пусть Tj,;=1, 2, ...,- п е р и о д ы занятости системы (т. е. длины интервалов времени в течение к-рых w(t)>0). Тогда для рассматриваемых систем
Пусть Tj,;=1, 2, ...,- п е р и о д ы занятости системы (т. е. длины интервалов времени в течение к-рых w(t)>0). Тогда для рассматриваемых систем 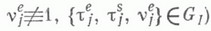
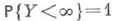 (это всегда при
(это всегда при 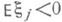 ), то справедливо следующее факторизационное тождество
), то справедливо следующее факторизационное тождество 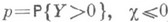 - величина первой неположительной суммы среди x1, x1+x2, ... Это соотношение позволяет отождествить с
- величина первой неположительной суммы среди x1, x1+x2, ... Это соотношение позволяет отождествить с 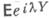 отношение
отношение 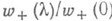 в любом тождестве
в любом тождестве  - функции ограниченной вариации). Равенство (5).осуществляет т. н. V-факторизацию функции
- функции ограниченной вариации). Равенство (5).осуществляет т. н. V-факторизацию функции 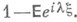 Оно позволяет указать следующие случаи, когда возможно отыскание
Оно позволяет указать следующие случаи, когда возможно отыскание 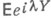 в явном виде.
в явном виде. и обозначают
и обозначают 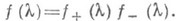
 -рациональная функция:
-рациональная функция: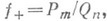 где Р т к Qn- многочлены степеней ти n соответст-
где Р т к Qn- многочлены степеней ти n соответст-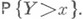
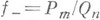 - рациональная функция, то функция (i-f)Qn в области Iml>0 имеет n-1 нулей l1, ..., ln-1 и
- рациональная функция, то функция (i-f)Qn в области Iml>0 имеет n-1 нулей l1, ..., ln-1 и 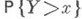 при
при  Именно, если
Именно, если 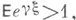 то определен единственный корень q>0 уравнения
то определен единственный корень q>0 уравнения 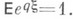 В этом случае при
В этом случае при 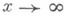
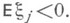 Тогда для слабой сходимости
Тогда для слабой сходимости 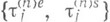 и
и 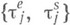 таковы, что
таковы, что 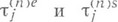 независимы, а распределения
независимы, а распределения 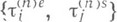 слабо сходятся к распределениям
слабо сходятся к распределениям 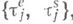 , то для выполнения (6) достаточно, чтобы
, то для выполнения (6) достаточно, чтобы 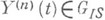 сходятся к распределениям
сходятся к распределениям  и последовательность
и последовательность 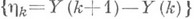 эргодична,
эргодична,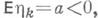 то для сходимости распределений
то для сходимости распределений 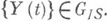 Тогда говорят, что система имеет большую нагрузку, если
Тогда говорят, что система имеет большую нагрузку, если 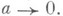 Пусть Х а(t).удовлетворяют условиям слабой зависимости, обеспечивающим при
Пусть Х а(t).удовлетворяют условиям слабой зависимости, обеспечивающим при  выполнение условий
выполнение условий  справедливо
справедливо 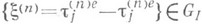 (также в схеме серий по параметру п), потребовав, чтобы
(также в схеме серий по параметру п), потребовав, чтобы 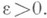 Тогда если
Тогда если 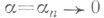 при
при  не меняя знака, так что
не меняя знака, так что 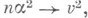 то
то 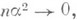 то
то 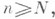 получают отказ и выбывают из рассмотрения. В этом случае
получают отказ и выбывают из рассмотрения. В этом случае 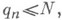 а вероятность
а вероятность 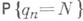 будет также вероятностью того, что n-й вызов получил отказ.
будет также вероятностью того, что n-й вызов получил отказ. и последовательность
и последовательность 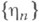 метрически транзитивна. Пусть, кроме того, выполнено следующее условие: или
метрически транзитивна. Пусть, кроме того, выполнено следующее условие: или 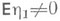 или
или 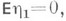 но во втором случае hn не представимы в виде
но во втором случае hn не представимы в виде 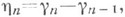 где
где  При выполнении этих условий существует предельное распределение q п при
При выполнении этих условий существует предельное распределение q п при 
 (это имеет место, напр., в случае, когда
(это имеет место, напр., в случае, когда  а остальные управляющие последовательности принадлежат G), то можно найти явный вид стационарного распределения для qn при
а остальные управляющие последовательности принадлежат G), то можно найти явный вид стационарного распределения для qn при 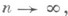 поскольку в этом случае qn связаны в простую однородную цепь Маркова с конечным числом состояний.
поскольку в этом случае qn связаны в простую однородную цепь Маркова с конечным числом состояний.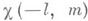 - положение частицы, вышедшей из О и блуждающей со скачками hk, k=1, 2, ..., в момент ее первого выхода за пределы интервала (-l, т). Если
- положение частицы, вышедшей из О и блуждающей со скачками hk, k=1, 2, ..., в момент ее первого выхода за пределы интервала (-l, т). Если 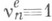 (т. е. если
(т. е. если 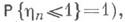 . то вероятности (9) могут быть явным образом выражены через распределения
. то вероятности (9) могут быть явным образом выражены через распределения 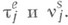
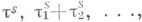 где
где 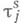 - элементы управляющей последовательности. Таким образом, вызов, заставший систему свободной, должен ждать до начала очередного этапа обслуживания.
- элементы управляющей последовательности. Таким образом, вызов, заставший систему свободной, должен ждать до начала очередного этапа обслуживания.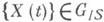 и эргодичен,
и эргодичен,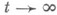 к распределению стационарного процесса
к распределению стационарного процесса 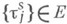 или
или 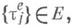 а остальные управляющие подпоследовательности принадлежат G1, то можно указать явные формулы для распределения
а остальные управляющие подпоследовательности принадлежат G1, то можно указать явные формулы для распределения