|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМАЗначение МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА в математической энциклопедии: понятие, к-рое включает в себя случайный "входящий" поток требований (вызовов, клиентов), нуждающихся в "обслуживании", и механизм (алгоритм), осуществляющий это "обслуживание". Типичным примером М. о. с. являются автоматич. телефонные станции, на к-рые случайным образом поступают требования - вызовы абонентов (входящий поток вызовов), а механизм обслуживания состоит из фиксированного числа n каналов (линий) связи, каждый из к-рых остается занятым под обслуживание очередного вызова случайное время, равное длительности разговора. Если все пканалов заняты, то вызов получает "отказ". Механизм (алгоритм) обслуживания может включать в себя также указания, на какую из свободных линий следует направлять очередной вызов, предложение ждать, если требуемый абонент занят, и др. Существуют и системы другого типа, когда каждое требование непременно должно быть обслужено, как ато имеет место, напр., в потоке самолетов, прибывающих в аэропорт для посадки, пли в потоке задач (программ), к-рые должны быть реализованы на электронно-вычислительной машине. "Случайную" часть М. о. с. удобно описывать с помощью случайных последовательностей или процессов. Наиболее простые М. о. с. можно описывать двумерными управляющими случайными последовательностями  неотрицательных случайных величин. Последовательность  в к-рые в систему поступают требования, подлежащие обслуживанию. Эквивалентным образом входной поток можно характеризовать случайным процессом Весьма распространено описание управляющих последовательностей с помощью маркированных точечных процессов, в к-рых Задание управляющей последовательности не определяет однозначно поведение системы. Необходимо задать "еще алгоритм обслуживания - правило, которое определяет моменты начала обслуживания и поведение вызовов в зависимости от состояния системы. Многообразие алгоритмов обслуживания порождает чрезвычайно много различных видов систем обслуживания. Ниже приведена классификация простейших из них. I. Системы с ожиданием (или системы с очередь ю). Вызовы, поступившие в систему и не принятые немедленно к обслуживанию, накапливаются, образуя "очередь", ожидающую обслуживания. В дальнейшем вызовы обслуживаются в порядке поступления. Система занята в момент времени t, если в этот момент есть очередь или происходит обслуживание очередного вызова. В противном случае система наз. свободной в момент времени t. Различают два типа систем с очередью. I1. Обычные системы. Если система свободна, то она начинает действовать (обслуживать очередной вызов) немедленно при поступлении вызова. Если система занята, то обслуживание очередного вызова начинается после окончания обслуживания предыдущего. Такие системы наз. также п о л н о д о с т у п н ы м и. I2. Системы с автономным обслуживанием. Здесь обслуживание начинается только в моменты времени II. Системы с ограниченной очередью. Считают, что длина q(t).очереди в момент tравна Рассматривают также системы со случайной ограниченной очередью и системы со случайным ограниченным временем ожидания. III. Системы с ограниченной очередью в случае N=1 наз. системами с отказами. Для систем с отказами автономное обслуживание обычно не рассматривается. В каждом из рассмотренных простейших видов систем задание управляющей последовательности полностью определяет эволюцию системы. Другими словами, для каждого элементарного события w и любого tоднозначно определено состояние системы к моменту времени t. Помимо перечисленных выше типов систем обслуживания, возможны и другие, более сложные системы. Они связаны с более сложными управляющими последовательностями и алгоритмами обслуживания. IV. Групповой входной поток и групповое обслуживание. Управление такими системами может происходить с помощью четырехмерных управляющих последовательностей  где Для систем с групповым входом и обслуживанием возможны те же алгоритмы обслуживания, к-рые были описаны выше. V. Многоканальные системы. В таких системах обслуживание может вестись одновременно в Многоканальная система наз. системой с отказами, если вызовы, в момент прихода к-рых все каналы оказались занятыми, получают отказ и выбывают из рассмотрения. Иногда для того чтобы упростить природу управляющих последовательностей для многоканальных систем, удобно задавать не две, a m+1 управляющих двумерных последовательностей  так что k- йканал обслуживания управляется последовательностью Приведенная классификация охватывает далеко не все виды систем обслуживания. Широкое распространение имеют, напр., системы, у к-рых вызовы подразделяются на два или более типов и одни типы имеют приоритет в обслуживании перед другими (такая ситуация возникает, когда стоимость простоя одних вызовов выше, чем у других). Характеризация таких систем требует введения в рассмотрение нескольких входящих потоков вызовов - по числу типов требований. К системам с приоритетным обслуживанием можно отнести также системы, у к-рых обслуживающее устройство требует перерывов в работе. Закон появления и длительности перерывов можно характеризовать специальным входным потоком. В литературе по массового обслуживания теории рассмотрены и др. специальные виды систем обслуживания. Однако при этом следует иметь в виду, что: 1) основные и наиболее распространенные типы М. о. с. находятся в рамках приведенной выше классификации; 2) методы исследования М. о. с. для различных систем, как правило, отличаются мало и в достаточной степени иллюстрируются методами изучения "основных" систем; в основе этих методов лежит аппарат теории вероятностей, как общие его разделы, так и специально разработанные. Основной целью изучения является исследование распределений различных параметров, характеризующих состояние системы (напр., длины очереди, времени ожидания начала обслуживания, вероятности данному вызову получить отказ и т. д.). Главный интерес при этом представляют эргодич. теоремы, описывающие поведение указанных характеристик через большой промежуток времени. Напр., одной из характеристик эффективности работы автоматической телефонной станции является доля вызовов, получивших отказ, т. е. предел рпри Метод исследования часто состоит в отыскании марковских процессов или последовательностей, характеризующих состояние системы. Если, напр., случайные величины В более сложных случаях приходится использовать асимптотич. методы (см. Массового обслуживания теория).или прибегать к моделированию случайных процессов, описывающих поведение М. о. с., по Монте-Карло методу. В статьях Массового обслуживания система с ожиданием и одним каналом обслуживания, Массового обслуживания система с ожиданием многоканальная, Массового обслуживания система с отказами, Массового обслуживания система (входящий поток вызовов) более подробно рассматриваются основные виды систем обслуживания и входные потоки. В этих статьях приняты следующие обозначения. Е - класс последовательностей независимых случайных величин с показательным распределением. Запись Запись Класс стационарных в узком смысле последовательностей обозначен GS. Приведенные обозначения могут применяться и к многомерным последовательностям. Напр., Для простоты изложения, как правило, ограничиваются рассмотрением "ординарных" входных и выходных процессов, когда Кроме того, природа управляющих последовательностей будет простой и однородной, если выделять из них начальные условия. Именно, рассматривают управляющие последовательности Лит. см. при СТ. Массового обслуживания теория. А. А. Боровков. |
|
|
|

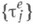 определяет поток вызовов е:она указывает случайные моменты времени
определяет поток вызовов е:она указывает случайные моменты времени 
 значение е(t).указывает число вызовов, поступивших в систему к моменту времени t. Вторая последовательность
значение е(t).указывает число вызовов, поступивших в систему к моменту времени t. Вторая последовательность  описывает процесс обслуживания s: случайная величина
описывает процесс обслуживания s: случайная величина  означает время, к-рое тратится на обслуживание вызова с номером j. Обслуженные вызовы выбывают из рассмотрения.
означает время, к-рое тратится на обслуживание вызова с номером j. Обслуженные вызовы выбывают из рассмотрения. представляют собой интервалы между точками, а
представляют собой интервалы между точками, а  - марки этих точек.
- марки этих точек.
 если один вызов в этот момент находится на обслуживании и п -1 вызовов ждут обслуживания. Пусть
если один вызов в этот момент находится на обслуживании и п -1 вызовов ждут обслуживания. Пусть 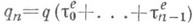 длина очереди в момент прихода n-го вызова (без учета этого вызова). В системах с ограниченной очередью вызов с номером п"получает отказ" и выбывает из рассмотрения, если в момент его прихода длина q п очереди оказывается равной максимальному допустимому значению
длина очереди в момент прихода n-го вызова (без учета этого вызова). В системах с ограниченной очередью вызов с номером п"получает отказ" и выбывает из рассмотрения, если в момент его прихода длина q п очереди оказывается равной максимальному допустимому значению  Число Nявляется существенной характеристикой системы. Если
Число Nявляется существенной характеристикой системы. Если  то получаются обычные системы с неограниченной очередью.
то получаются обычные системы с неограниченной очередью. - неотрицательны и целочисленны. Смысл новых переменных следующий: вызовы поступают группами объемов
- неотрицательны и целочисленны. Смысл новых переменных следующий: вызовы поступают группами объемов  (соответственно в моменты времени
(соответственно в моменты времени  ); обслуживание также происходит группами: в первой партии обслуживается
); обслуживание также происходит группами: в первой партии обслуживается  вызовов, во второй
вызовов, во второй  вызовов и т. д. (объемы этих групп могут быть и меньше, если в очереди не окажется достаточного количества вызовов). При этом на обслуживание k- йпартии тратится время
вызовов и т. д. (объемы этих групп могут быть и меньше, если в очереди не окажется достаточного количества вызовов). При этом на обслуживание k- йпартии тратится время 
 каналах, так что обслуживание очередного вызова (или партии вызовов при групповом обслуживании) может начаться прежде, чем закончится обслуживание предыдущей. Алгоритмы обслуживания многоканальных систем выглядят аналогично для всех рассмотренных типов обслуживания (каждый канал действует как самостоятельное обслуживающее устройство). Надо лишь дополнить эти алгоритмы указаниями, в какой канал должны направляться вызовы, если свободными оказались одновременно несколько каналов. При этом по-прежнему на обслуживание i-й партии (объема
каналах, так что обслуживание очередного вызова (или партии вызовов при групповом обслуживании) может начаться прежде, чем закончится обслуживание предыдущей. Алгоритмы обслуживания многоканальных систем выглядят аналогично для всех рассмотренных типов обслуживания (каждый канал действует как самостоятельное обслуживающее устройство). Надо лишь дополнить эти алгоритмы указаниями, в какой канал должны направляться вызовы, если свободными оказались одновременно несколько каналов. При этом по-прежнему на обслуживание i-й партии (объема  ) тратится время
) тратится время 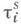
 Напр.,
Напр.,  есть время обслуживания партии вызовов, к-рая является i-й в k- мканале.
есть время обслуживания партии вызовов, к-рая является i-й в k- мканале. (если он существует) отношения r(t)/e(t).числа r(t).вызовов, потерянных за время t, к общему числу e(t).вызовов, поступивших за это время. Этот предел можно с достаточными на то основаниями называть вероятностью отказа. Показателями, характеризующими системы с ожиданием, являются предельные при
(если он существует) отношения r(t)/e(t).числа r(t).вызовов, потерянных за время t, к общему числу e(t).вызовов, поступивших за это время. Этот предел можно с достаточными на то основаниями называть вероятностью отказа. Показателями, характеризующими системы с ожиданием, являются предельные при  распределения вероятностей
распределения вероятностей  для времени wn, к-рое n-й вызов ожидал начала обслуживания с момента прихода, и для длины q п очереди в момент появления в системе n-го вызова.
для времени wn, к-рое n-й вызов ожидал начала обслуживания с момента прихода, и для длины q п очереди в момент появления в системе n-го вызова. и
и 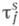 показательно распределены и при разных индексах независимы, то "процесс очереди" q(t).будет марковским и допускает описание с помощью простых дифференциальных уравнений для стационарного распределения. В других случаях обычно пытаются построить случайные моменты времени t1, t2, ... такие, что q(tn).или значения других характеристик (напр., времени ожидания), взятые в моменты t1, t2, ..., образовывали бы цепь Маркова. Это т. н. метод вложенной цепи Маркова. Этот метод часто используется в модифицированном виде, когда строятся полумарковские процессы, описывающие интересующие нас состояния системы.
показательно распределены и при разных индексах независимы, то "процесс очереди" q(t).будет марковским и допускает описание с помощью простых дифференциальных уравнений для стационарного распределения. В других случаях обычно пытаются построить случайные моменты времени t1, t2, ... такие, что q(tn).или значения других характеристик (напр., времени ожидания), взятые в моменты t1, t2, ..., образовывали бы цепь Маркова. Это т. н. метод вложенной цепи Маркова. Этот метод часто используется в модифицированном виде, когда строятся полумарковские процессы, описывающие интересующие нас состояния системы.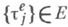 означает, что
означает, что 
 означает, что случайные величины
означает, что случайные величины  независимы и одинаково распределены (само распределение может быть произвольным). Соотношения вида
независимы и одинаково распределены (само распределение может быть произвольным). Соотношения вида  или
или 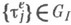 обычно предполагают также, что управляющая последовательность
обычно предполагают также, что управляющая последовательность  не зависит от остальных управляющих последовательностей.
не зависит от остальных управляющих последовательностей. означает, что двумерная последовательность стационарна и составлена из независимых векторов.
означает, что двумерная последовательность стационарна и составлена из независимых векторов. (вызовы поступают и обслуживаются по одному). Возможности обобщений на "неординарный" случай (вызовы поступают и обслуживаются группами:
(вызовы поступают и обслуживаются по одному). Возможности обобщений на "неординарный" случай (вызовы поступают и обслуживаются группами:  или
или 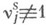 ) оговаривают отдельно.
) оговаривают отдельно. при
при  и считают, что q(0)=0, а первый вызов пришел в систему в момент
и считают, что q(0)=0, а первый вызов пришел в систему в момент  Если управление задается входным процессом e(t), то фиксация
Если управление задается входным процессом e(t), то фиксация  не производится.
не производится.