|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАССА И КОМАССАЗначение МАССА И КОМАССА в математической энциклопедии: - сопряженные норма в нек-рых двойственных друг другу векторных пространствах. 1)Масса r-вектопага - a число  ai- простые r-векторы}. Ко масса r-ковектора со - число  - простые r-векторы, |a| = 1}. - простые r-векторы, |a| = 1}. Здесь Масса |a|0 и комасса | w|0 - сопряженные нормы соответственно в пространствах r-векторов V[r], и r-ковекторов  и равенства имеют место в том и только в том случае, когда a(w) - простой r-(ко)вектор;  для внешних произведений если 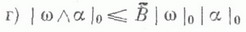 для внутренних произведений 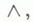 причем  при  Эти определения позволяют определить М. и к. для сечений соответствующих расслоений, стандартными слоями к-рых являются  2) Масса полиэдральной цели  где 3) К о м а с с а (бемольной, в частности диезной) коцепи Xопределяется стандартным образом:  где А - полиэдральная цепь, Лит. см. при ст. Бемольная норма. М. И. Войцеховский. |
|
|
|

 - стандартная норма r-вектора,
- стандартная норма r-вектора,  - скалярное произведение вектора и ковектора.
- скалярное произведение вектора и ковектора. при этом:
при этом: причем для простого поликовектора w (или x) В=1, а в общем случае
причем для простого поликовектора w (или x) В=1, а в общем случае 
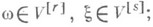
 Напр., комасса формы w в области
Напр., комасса формы w в области  равна
равна 
 равна
равна  - объем клетки
- объем клетки  Для произвольной цепи массу (конечную или бесконечную) можно определить несколькими способами, к-рые для бемольной цепи (см. Бемольная норма).и диезной цепи (см. Диезная норма )дают одно и то же значение массы.
Для произвольной цепи массу (конечную или бесконечную) можно определить несколькими способами, к-рые для бемольной цепи (см. Бемольная норма).и диезной цепи (см. Диезная норма )дают одно и то же значение массы. - значение коцепи Xна цепи А.
- значение коцепи Xна цепи А.