|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАРТИНГАЛЗначение МАРТИНГАЛ в математической энциклопедии: - стохастическая последовательность  (с вероятностью 1, или почти наверное). В случае дискретного времени T={1, 2, ...}, в случае непрерывного времени  и супермартингал, для к-рых и супермартингал, для к-рых  Пример 1. Если Пример 2. Пусть Y=(Yn, Fn) - М. (субмартингал), V=(Vn, Fn) - нек-рая предсказуемая последовательность (т. е. Vn являются не только Fn -измеримыми, но и Fn-1 -измеримыми, Тогда если величины (VY)Fn интегрируемы, то стоха-стич. последовательность ((VY)n-1, Fn )образует М. (субмартингал). В частности, если  и  то((VY)n, Fn).образует М. Эта стохастич. последовательность служит математич. моделью игры, в к-рой игрок выигрывает единицу капитала, если xk=+1, и проигрывает единицу, если xk=-1, a Vk - величина его ставки в k-й партии. Игровой смысл функции Vk, определяемой равенством (2), состоит в том, что игрок увеличивает ставку вдвое при проигрыше п прекращает игру при первом выигрыше. Такая система игры в игровой практике носит название М., что н послужило причиной возникновения математич. термина "мартингал". Один из основных фактов теории М. состоит в том, что структура М. (субмартингалов) Х=(Xt, Ft).сохраняется при случайной замене времени. Точная формулировка этого факта (называемого теоремой о преобразовании свободного выбора) состоит в следующем: если t1 и t2 - два конечных марковских момента,  то В качестве частного случая отсюда следует Вальда тождество:  К числу основных результатов теории М. относятся неравенства Дуба: если Х=( Х n, Fn) - неотрицательный субмартингал,  то  Если Х=Х=( Х n, Fn) - М., то для случая p>1 справедливы неравенства Буркхольдера (обобщающие неравенства Хинчина и Марцинкевича - Зигмунда для сумм независимых случайных величин):  где А р и В р - нек-рые универсальные константы (не зависящие от Xи от п). в качестве к-рых можно взять  и  С учетом (5) из (7) следует, что (р>1)  где  На случай р=1 обобщаются неравенства (8). Именно, имеют место неравенства Дэвиса: существуют такие универсальные постоянные Аи В, что  Для доказательства разного рода теорем о сходимости субмартпнгалов с вероятностью единица ключевую роль играет неравенство Дуба для математического ожидания  Основной результат о сходимости субмартингалов содержится в теореме Дуба: если Х=( Х п, Fn) - субмартингал и sup субмартингал Xравномерно интегрируемый, то помимо сходимости с вероятностью единица имеет место и сходимость в смысле L1 т. е.  Следствием этого результата является теорема Леви о непрерывности условных математических ожиданий: если  где  Естественным обобщением М. является понятие локального мартингала, т. е. такой стохастич. последовательности Х=( Х t, Ft), для к-рой найдется последовательность  являются М. В случае дискретного времени каждый локальный М. Х=( Х п, Fn )есть мартингал ь-ное преобразование, т. е. представим в виде Х п=(VY) п, где V - нек-рая предсказуемая последовательность, а Y - нек-рый М. Каждый субмартингал Х=( Х t, Ft )допускает и притом единственное разложение Дуба - Мейера Х t=Mt+At, где M=(Mt,Ft) - M., a А=(At, Ft).-предсказуемый процесс. В частности, если m=(mt, Ft) - квадратично-интегрируемый М., то его квадрат зуемого процесса V=(Vt, Ft).таких, что  (с вероятностью 1, или почти наверное), t> 0, можно определить стохастич. интеграл  к-рый является локальным М. В случае винеровского процесса W=(Wt, Ft), являющегося квадратично-интегрируемым М., <m>t=t и стохастич. интеграл (VW)t есть не что иное, как стохастич. интеграл Ито по винеровскому процессу, В случае непрерывного времени неравенства Дуба, Буркхольдера и Дэвиса также остаются в силе (для процессов непрерывных справа и имеющих пределы слева). Лит.:[1] Д у б Д ж., Вероятностные процессы, пер. с англ., М., 1956; [2] Ги х м а н И. И., Скороход А. В., Теория случайных процессов, т. 1, М., 1971. А. Н. Ширяев. |
|
|
|

 заданная на вероятностном пространстве
заданная на вероятностном пространстве  с выделенным на нем неубывающим семейством s-алгебр
с выделенным на нем неубывающим семейством s-алгебр  такая, что
такая, что  Xt являются Ft -измеримыми и
Xt являются Ft -измеримыми и  Родственными понятиями являются стохастич. последовательности, образующие субмартингал, для к-рых
Родственными понятиями являются стохастич. последовательности, образующие субмартингал, для к-рых  - последовательность независимых случайных величин с
- последовательность независимых случайных величин с  то X = ( Х n, Fn).с
то X = ( Х n, Fn).с  является М.,
является М.,
 и
и 
 - последовательность независимых случайных величин, соответствующих схеме Бернулли
- последовательность независимых случайных величин, соответствующих схеме Бернулли  и
и 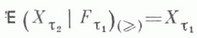 (с вероятностью 1, или почти наверное), где
(с вероятностью 1, или почти наверное), где 
 числа пересечений bn(a, b).субмартингалов Х=( Х п, Fn).интервала [ а, b]снизу вверх за пшагов
числа пересечений bn(a, b).субмартингалов Х=( Х п, Fn).интервала [ а, b]снизу вверх за пшагов  то с вероятностью единица существует
то с вероятностью единица существует  Если
Если  то
то  конечных марковских моментов,
конечных марковских моментов,  (с вероятностью 1 или почти наверное),
(с вероятностью 1 или почти наверное),  таких, что для каждого
таких, что для каждого  "остановленные" последовательности
"остановленные" последовательности  является субмартингалом, для к-рого в его разложении Дуба - Мейера
является субмартингалом, для к-рого в его разложении Дуба - Мейера  процесс <m>=(<m>t, Ft).наз. квадратической характеристикой мартингала т. Для каждого квадратично-интегрируемого М. ти предска-
процесс <m>=(<m>t, Ft).наз. квадратической характеристикой мартингала т. Для каждого квадратично-интегрируемого М. ти предска-