"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АСИМПТОТИЧЕСКАЯ ПРЕНЕБРЕГАЕМОСТЬЗначение АСИМПТОТИЧЕСКАЯ ПРЕНЕБРЕГАЕМОСТЬ в математической энциклопедии:
свойство случайных величин, указывающее на их индивидуально малый вклад в качестве отдельных компонент в их сумму. Это понятие существенно, напр., в так наз. схемах серий. Именно, пусть случайные величины  взаимно независимы при каждом n, и взаимно независимы при каждом n, и

Если для любых  и и  при достаточно больших пвыполняется неравенство при достаточно больших пвыполняется неравенство 
то отдельные слагаемые  наз. А. п. (величины наз. А. п. (величины  образуют при этом так наз. нулевую схему серий). При условии (1) справедлив следующий важный результат: класс предельных распределений для образуют при этом так наз. нулевую схему серий). При условии (1) справедлив следующий важный результат: класс предельных распределений для  ( ( - нек-рые "центрирующие" константы) совпадает с классом безгранично делимых распределений. Если распределения - нек-рые "центрирующие" константы) совпадает с классом безгранично делимых распределений. Если распределения 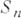 сходятся к предельному, сходятся к предельному, и слагаемые одинаково распределены, то условие (1) автоматически выполняется. Если усилить требование А. п., предполагая, что для любых и слагаемые одинаково распределены, то условие (1) автоматически выполняется. Если усилить требование А. п., предполагая, что для любых  и и  при всех достаточно больших п при всех достаточно больших п
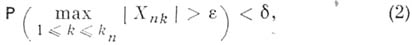
то будет верно утверждение: при условии (2) предельным распределением для 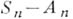 может быть только нормальное распределение (в частности, с дисперсией, равной нулю, т. е. вырожденное распределение). А. <В. Прохоров. может быть только нормальное распределение (в частности, с дисперсией, равной нулю, т. е. вырожденное распределение). А. <В. Прохоров.
|

 взаимно независимы при каждом n, и
взаимно независимы при каждом n, и 
 и
и  при достаточно больших пвыполняется неравенство
при достаточно больших пвыполняется неравенство 
 наз. А. п. (величины
наз. А. п. (величины  образуют при этом так наз. нулевую схему серий). При условии (1) справедлив следующий важный результат: класс предельных распределений для
образуют при этом так наз. нулевую схему серий). При условии (1) справедлив следующий важный результат: класс предельных распределений для  (
( - нек-рые "центрирующие" константы) совпадает с классом безгранично делимых распределений. Если распределения
- нек-рые "центрирующие" константы) совпадает с классом безгранично делимых распределений. Если распределения 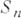 сходятся к предельному,
сходятся к предельному, и слагаемые одинаково распределены, то условие (1) автоматически выполняется. Если усилить требование А. п., предполагая, что для любых
и слагаемые одинаково распределены, то условие (1) автоматически выполняется. Если усилить требование А. п., предполагая, что для любых  и
и  при всех достаточно больших п
при всех достаточно больших п 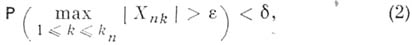
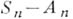 может быть только нормальное распределение (в частности, с дисперсией, равной нулю, т. е. вырожденное распределение). А. <В. Прохоров.
может быть только нормальное распределение (в частности, с дисперсией, равной нулю, т. е. вырожденное распределение). А. <В. Прохоров.