|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
МАКСИМУМА ПРИНЦИПЗначение МАКСИМУМА ПРИНЦИП в математической энциклопедии: дискретный- принцип максимума Понтрягина для дискретных по времени процессов управления. Для такого процесса М. п. может не выполняться, хотя для его непрерывного аналога, получающегося заменой конечно разностного оператора  Задачу (1) - (4) можно трактовать как обычную задачу на экстремум при наличии ограничений. Тогда условия оптимальности траектории  где выражение  по аналогии с непрерывным случаем наз. Гамильтона функцией. Пусть функции J, ft, 2=0, 1, ..., Т, дифференцируемы по совокупности переменных, а множество Uограничено и замкнуто. Тогда для того чтобы решение  для всех допустимых вариаций управления  Третье условие - к условию для первой вариации функции Гамильтона:  Однако условие (5) не означает, что функция Гамильтона на оптимальном управлении достигает максимума  по всем управлениям, удовлетворяющим ограничениям (3); оно показывает, что в частности, когда  Построены примеры, в к-рых оптимальное управление  или по управлениям 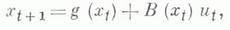 при дополнительном условии линейности критерия Трактуя задачу оптимального управления линейной дискретной системой как задачу линейного программирования (см. [6], [7]), можно получить двойственную ей динамич. <задачу с дискретным временем. Сопряженная система для импульсов дает уравнения динамики для двойственной динамич. задачи. На оптимальной траектории совпадают не только критерии, но и функции Гамильтона двойственных динамич. задач. Лит.:[1] Фан Лянь-цэнь, Ван Чу-сен, Дискретный принцип максимума, пер. с англ., М., 1967; [2] Пропой А. И., Элементы теории оптимальных процессов, М., 1973; [3] П ш е н и ч н ы й Б. Н., Необходимые условия экстремума, М., 1969; [4] Б о л т я н с к и й В. Г., Оптимальное управление дискретными системами, М., 1973; [5] Габасов Р., К и-р и л л о в а Ф. М., "Автоматика и телемеханика", 1966, № 11, с. 46-51; [6] И в а н и л о в Ю. П., "Прикл. матем. и программирование", Киш., 1971, в. 4, с. 31 - 40; [7] И в а н и л о в Ю. П., Пропой А. И., "Докл. АН СССР", 1971, т. 198, М5, с. 1011-1014. Ю. П. Иванилов. |
|
|
|

 на дифференциальный dx/dt, Понтрягина принцип максимума справедлив. Пусть, напр., имеется задача оптимального управления
на дифференциальный dx/dt, Понтрягина принцип максимума справедлив. Пусть, напр., имеется задача оптимального управления  можно получить с помощью Лагранжа функции
можно получить с помощью Лагранжа функции задачи (1) - (4) было оптимальным, необходимо существование Лагранжа множителей
задачи (1) - (4) было оптимальным, необходимо существование Лагранжа множителей  таких, что точка
таких, что точка  будет стационарной точкой функции Лагранжа, т. е. в этой точке выполняются условия
будет стационарной точкой функции Лагранжа, т. е. в этой точке выполняются условия  Первое условие приводит к уравнениям динамики дискретного процесса (2) и начальному условию (4). Второе - к граничному условию и сопряженной системе для импульсов {pt+1}:
Первое условие приводит к уравнениям динамики дискретного процесса (2) и начальному условию (4). Второе - к граничному условию и сопряженной системе для импульсов {pt+1}: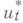 - стационарная точка функции Гамильтона. Если первая вариация функции Гамильтона
- стационарная точка функции Гамильтона. Если первая вариация функции Гамильтона  обращается в нуль (это имеет место,
обращается в нуль (это имеет место, - внутренняя точка множества или когда в точке
- внутренняя точка множества или когда в точке  существуют допустимые вариации управления
существуют допустимые вариации управления  ортогональные
ортогональные  ), то характер стационарной точки определяется следующими по порядку членами в разложении:
), то характер стационарной точки определяется следующими по порядку членами в разложении: является точкой локального максимума, локального минимума и даже седловой точкой функции Гамильтона. Таким образом, в общем случае для дискретных систем принцип максимума не имеет места. Для систем, линейных по фазовым переменным
является точкой локального максимума, локального минимума и даже седловой точкой функции Гамильтона. Таким образом, в общем случае для дискретных систем принцип максимума не имеет места. Для систем, линейных по фазовым переменным  в первом или выпуклости множества Uво втором случае принцип максимума выполняется (см. [1] - [5]).
в первом или выпуклости множества Uво втором случае принцип максимума выполняется (см. [1] - [5]).