" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

МАКДОНАЛЬДА ФУНКЦИЯ

Значение МАКДОНАЛЬДА ФУНКЦИЯ в математической энциклопедии:

модифицированная цилиндрическая функция, бесселева функция мнимого аргумента, - функция

где v - произвольное нецелое действительное число,

- цилиндрич. функция чисто мнимого аргумента. Рассмотрена X. Макдональдом [1]. Если п - целое число, то

М. ф. К _v(z) является решением дифференциального уравнения

стремящимся экспоненциально к нулю, когда при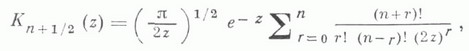нимая положительные значения. Функции I_v(z) и К _v(z) образуют фундаментальную систему решений уравнения (*).

При функция К _v(z) имеет корни лишь в случае Re(z)<0. Если то число всех корней в этих двух квадрантах равно ближайшему к четному числу, если только не является целым; в последнем случае число всех корней равно

При корней нет, если только не целое. Ряды и асимптотич. представления:

n - целое неотрицательное;

z велико и Рекуррентные формулы:

Лит.:[1] М а с d о h а l d Н. М., "Proc. London Math. Soc.", 1899, v. 30, p. 165-79; [2] В а т с о н Г. Н., Теория бесселевых Функций, пер. с англ., ч. 1, М., 1949. В. И. Пагурова.