|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛЯПУНОВА - ШМИДТА УРАВНЕНИЕЗначение ЛЯПУНОВА - ШМИДТА УРАВНЕНИЕ в математической энциклопедии: нелинейное интегральное уравнение вида 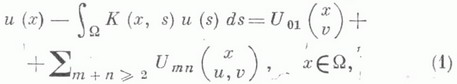 где
  - ограниченное замкнутое множество конечномерного евклидова пространства, v и функции К - заданные непрерывные функции своих аргументов - ограниченное замкнутое множество конечномерного евклидова пространства, v и функции К - заданные непрерывные функции своих аргументов 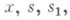 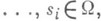 и - искомая функция. Сумма, входящая в правую часть равенства (1), может быть конечной или представлять бесконечный ряд. В последнем случае ряд наз. интегро-степенным рядом от двух функциональных аргументов. Предполагается, что этот ряд сходится абсолютно и равномерно. и - искомая функция. Сумма, входящая в правую часть равенства (1), может быть конечной или представлять бесконечный ряд. В последнем случае ряд наз. интегро-степенным рядом от двух функциональных аргументов. Предполагается, что этот ряд сходится абсолютно и равномерно. Если единица не является характеристич. числом ядра К( х, s), то уравнение (1) при достаточно малом: |v(x)|в классе непрерывных функций имеет единственное малое решение, представимое в виде интегро-степеннрго ряда. Случай, когда единица есть характеристич. число ядра К, является более сложным. В этом случае строится нек-рая система уравнений - уравнение разветвления: 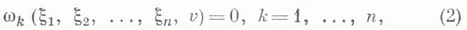 где wk - известные степенные ряды, n - кратность характеристич. числа 1. Система (2) в общем случае имеет неединственное решение. Какова бы ни была фиксированная достаточно малая функция v, каждому малому непрерывному решению системы (2) (непрерывное решение системы (2) наз. малым, если Уравнение типа (1) впервые было рассмотрено А. М. Ляпуновым в 1906, а позднее - в более общем виде - Э. Шмидтом (Е. Schmidt, 1908). Лит.:[1] В а й н б е р г М. М., Т р е н о г и н В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [2] Смирнов Н. С., Введение в теорию нелинейных интегральных уравнений, Л.- М., 1936. Б. В. Хведелидзе |
|
|
|

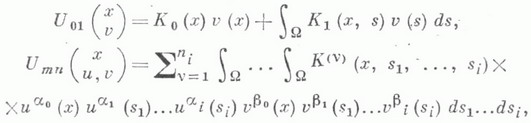
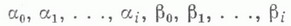 - неотрицательные целые числа,
- неотрицательные целые числа, ) соответствует малое решение уравнения (1), представимое в виде интегро-степенного ряда.
) соответствует малое решение уравнения (1), представимое в виде интегро-степенного ряда.