|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛЯПУНОВА ФУНКЦИЯЗначение ЛЯПУНОВА ФУНКЦИЯ в математической энциклопедии: - функция, определяемая следующим образов. Пусть х 0 - неподвижная точка системы дифференциальных уравнений (т. е. Л. ф. наз. дифференцируемая функция 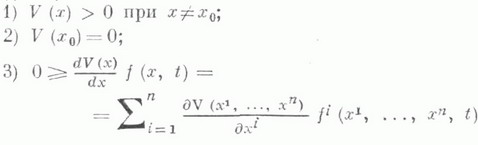 Функция V(х).введена А. М. Ляпуновым (см. [1]) Имеет место лемма Ляпунова: если Л. ф. существует, то неподвижная точка устойчива по Ляпунову. На этой лемме основан один из методов исследования устойчивости (т. н. второй метод Ляпунова). Лит.: [1] Л я п у в о в А. М., Собр. соч., Т. 2, М.- Л., 1956, с. 7-263; [2] Б а р б а ш и н Е. А., Функции Ляпунова, М., 1978. В. М. Миллионщиков. |
|
|
|


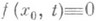 ), где отображение
), где отображение  непрерывной непрерывно дифференцируемо по х(здесь U - нек-рая окрестность точки х 0 в
непрерывной непрерывно дифференцируемо по х(здесь U - нек-рая окрестность точки х 0 в 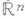 ); в координатах эта система записывается в виде
); в координатах эта система записывается в виде 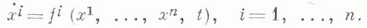
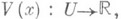 обладающая свойствами:
обладающая свойствами: