|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛУЗИНА ТЕОРЕМАЗначение ЛУЗИНА ТЕОРЕМА в математической энциклопедии: - 1) Л. т. в теории функций комплексного переменного (локальный принцип конечной площади) - результат Н. Н. Лузина, обнаруживающий связь между граничными свойствами аналитич. функций в единичном круге и метрикой римановых поверхностей, на к-рые они отображают круг (см. [1], [2]). Пусть V - любая область внутри единичного круга 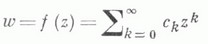 - регулярная аналитич. функция в D. Тогда, если площадь римановой поверхности, являющейся образом области Vпри отображении w=f(z), конечна, то ряд 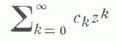 сходится почти всюду на дуге а. В связи с этой теоремой Н. Н. Лузин сформулировал гипотезу, известную также как проблема Лузина. Точку Лит.:[1] Лузин Н. Н., "Докл. АН СССР", 1947, т. 56, № 5, с. 447-50; [2] е г о же, Собр. соч., т. 1, М., 1953, с. 318-30; [3] Л о в а т е р А., в сб.: Итоги науки и техники. Математический анализ, т. 10, М., 1973, с. 99-259. Е. Д. Соломенцев. 2) Л. т. в дескриптивной теории множеств можно условно разбить на три цикла. Первый и основной цикл направлен на изучение эффективных множеств (аналитических, борелевских, лузинских (проективных) множеств). Сюда относится Лузина принципы отделимости и теорема о существовании Лузина множеств любого класса. Второй цикл представляет собой изучение задач, лежащих на пути к решению континуум-гипотезы и проблемы мощности СA -множеств. Здесь выделяется тео. <рема Лузина-Серпиньского о разбиении отрезка на 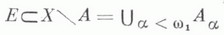 - разложение множества ХА на конституанты, тогда существует такой индекс 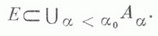 Третий цикл содержит результаты, полученные с использованием аксиомы выбора. Сюда же примыкают философские работы по теории множеств. Здесь выделяются Л. т. о существовании несчетного множества 1-й категории на всяком совершенном множестве, о разбиении интервала на несчетное множество неизмеримых множеств. Завершает этот цикл Л. т. о частях натурального ряда, отражающие нек-рые свойства нароста Б. А. Ефимов. |
|
|
|

 плоскости комплексного переменного z, примыкающая к нек-рой дуге а единичной окружности
плоскости комплексного переменного z, примыкающая к нек-рой дуге а единичной окружности 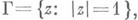 a
a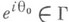 __ наз. точкой Лузина функции w=f(z), если w=f(z).отображает каждый круг, изнутри касающийся Г в точке
__ наз. точкой Лузина функции w=f(z), если w=f(z).отображает каждый круг, изнутри касающийся Г в точке 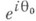 , на область бесконечной площади на римановой поверхности функции w=f(z). Гипотеза Лузина состоит в том, что существуют ограниченные аналитич. функции в Dтакие, что каждая точка Г является для них точкой Лузина. Гипотеза Лузина впервые была подтверждена полностью в 1955 (см. [3]).
, на область бесконечной площади на римановой поверхности функции w=f(z). Гипотеза Лузина состоит в том, что существуют ограниченные аналитич. функции в Dтакие, что каждая точка Г является для них точкой Лузина. Гипотеза Лузина впервые была подтверждена полностью в 1955 (см. [3]).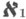 борелевских множеств, к-рое определяется соответствующим Лузина решетом, а также Л. т. о покрытии: пусть Еи А - непересекающиеся аналитич. множества и
борелевских множеств, к-рое определяется соответствующим Лузина решетом, а также Л. т. о покрытии: пусть Еи А - непересекающиеся аналитич. множества и 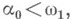 что
что 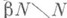 Стоуна - Чеха бикомпактного расширения
Стоуна - Чеха бикомпактного расширения 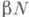 натурального ряда N. Лит.:[1] Л у зин Н. Н., Собр. соч., т. 2, М., 1958.
натурального ряда N. Лит.:[1] Л у зин Н. Н., Собр. соч., т. 2, М., 1958.