" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЛУЗИНА КРИТЕРИЙ

Значение ЛУЗИНА КРИТЕРИЙ в математической энциклопедии:

измеримости функции действительного переменного: для того чтобы функция f(х).почти всюду конечная, заданная на отрезке [ а, b], была измеримой, необходимо и достаточно, чтобы для любого 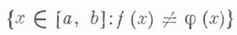существовала непрерывная на [ а, b]функция такая, что мера множества

была меньше е. Доказан Н. Н. Лузиным [1]. Другими словами, почти всюду конечная функция является измеримой тогда и только тогда, когда она становится непрерывной, если пренебречь множеством сколь угодно малой меры.

Лит.:[1] Лузин Н. Н., "С. r. Acad. sci.", 1912, t. 154, p. 1688-90; [2] Н а т а н с о н И. П., Теория функций вещественной переменной, 3 изд., М., 1974.

В. А. Ефимов.