|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОРЕНЦА ПРЕОБРАЗОВАНИЕЗначение ЛОРЕНЦА ПРЕОБРАЗОВАНИЕ в математической энциклопедии: преобразование координат, связывающее две галилеевы системы координат в каком-либо псевдоевклидовом пространстве;иными словами, Л. п. сохраняет квадрат т. н. интервала событий. Л. п. является аналогом ортогональных преобразований (или обобщением понятия движения) в евклидовом пространстве. Л. п. образуют группу, называемую группой Лоренца (или общей группой Лоренца), к-рая обозначается через L. Л. п. находят применение в четырехмерном пространстве-времени специальной теории относительности, для к-рого в галилеевых координатах х, у, z, tинтервал имеет вид 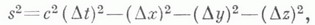 где с - скорость света в вакууме. Часто рассматривают более узкие классы Л. п. Так, Л. п., сохраняющие знак координаты t, образуют т. н. полную группу Лоренца Общая группа Л. п. состоит из комбинаций пространственных отражений, отражений во времени, пространственных поворотов и преобразований, к-рые с физич. точки зрения являются преобразованиями перехода от одной инерциальной системы отсчета к другой, движущейся относительно первой со скоростью V, а с ма-тематич. точки зрения - гиперболич. поворотом на угол y в плоскости с псевдоевклидовой метрикой. Наличие последнего типа преобразований является специфич. чертой группы Л. п. Для перехода от галилеевой системы координат х', у', z', t' к галилеевой системе координат х, у, z, t, движущейся относительно первой со скоростью Vпараллельно оси х', указанные преобразования имеют вид 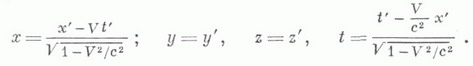 Если ввести угол гиперболического поворота y по формулам 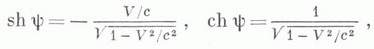 то Л. п. примут вид 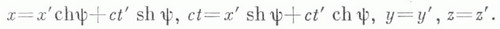 Эти преобразования часто наз. просто Л. п. Они не образуют группу: действие трех гиперболич. поворотов с непараллельными векторами скоростей может дать обычный пространственный поворот - т. н. т о м а с о в с к а я прецессия. Часто к общим Л. п. добавляют переносы начала координат, получая при этом т. н. преобразования Пуанкаре, образующие группу Пуанкаре. Свойства группы Л. п. сходны со свойствами ортогональных групп. Отличия связаны с наличием двух типов отражений (пространственных и временных) и с некомпактностью группы Л. п. (т. к. единичная сфера в псевдоевклидовом пространстве, т. е. множество точек, для к-рого модуль интервала до начала координат равен единице, некомпактна). Физические приложения Л. п. связаны с Эйнштейна относительности принципом, согласно к-рому все физич. законы, кроме законов гравитации, инвариантны относительно Л. п. В ряде случаев, напр. в аксиоматической квантовой теории поля, использование этого и других столь же общих постулатов позволяет делать далеко идущие выводы о видах функциональных зависимостей между различными физич. величинами. В различных областях физики (в особенности, в теории элементарных частиц) находят широкое применение представления групп Л. п. В соответствии с принципом относительности Эйнштейна физич. величины с различными законами преобразований - векторы, спиноры, тензоры - преобразуются по тем или иным представлениям группы Л. п. При этом оказывается, что эти представления можно характеризовать двумя инвариантами, к-рые отождествляются с массой и спином частиц, описываемых этой физич. величиной. Инфинитезимальные Л. п., т. е. повороты на бесконечно малый угол, часто используют для получения различных законов сохранения. Находят применения также Л. п. в касательном пространстве псевдориманова пространства; эти преобразования относятся к т. н. локальным симметриям. Л. п. получили свое название в связи с работами Г. Лоренца (Н. Lorentz) по электронной теории, к-рые сыграли важную роль в формулировании этого понятия. Лит.:[1] Л а н д а у Л. Д., Л и ф ш и ц Е. М., Теория поля, 6 изд., т. 2, М., 1973; [2] Н а й м а р к М. А., Линейные представления группы Лоренца, М., 1958; [3] Физический энциклопедический словарь, т. 3, М., 1963. Д. Д. Соколов. |
|
|
|

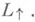 Л. п., матрицы к-рых имеют положительный определитель, наз. собственными преобразованиями Лоренца и образуют собственную группу Лоренца
Л. п., матрицы к-рых имеют положительный определитель, наз. собственными преобразованиями Лоренца и образуют собственную группу Лоренца 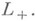 Пересечение
Пересечение 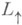 и
и 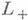 часто наз. просто группой Лоренца.
часто наз. просто группой Лоренца.