"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОКАЛЬНЫЙ УНИФОРМИЗИРУЮЩИЙ ПАРАМЕТР
Значение ЛОКАЛЬНЫЙ УНИФОРМИЗИРУЮЩИЙ ПАРАМЕТР в математической энциклопедии:
локальная у н и ф о р м и з и р у ю щ а я, локальный п а р а м е т р,- комплексное переменное t, определенное как непрерывная функция 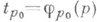 точки р римановой поверхности R всюду в нек-рой окрестности V(p0) точки
точки р римановой поверхности R всюду в нек-рой окрестности V(p0) точки  реализующая гомеоморфное отображение окрестности V(p0) на круг
реализующая гомеоморфное отображение окрестности V(p0) на круг  причем
причем  При этом V(p0) наз. отмеченной, или параметрической, окрестностью,
При этом V(p0) наз. отмеченной, или параметрической, окрестностью,
 - отмеченным, или параметрическим, отображением, D(р 0) - отмеченным, или параметрическим, к р у г о м. При отмеченном отображении любая функция точки g(p), определенная в отмеченной окрестности V(p0), переходит в функцию Л. у. п. t, т. е.
- отмеченным, или параметрическим, отображением, D(р 0) - отмеченным, или параметрическим, к р у г о м. При отмеченном отображении любая функция точки g(p), определенная в отмеченной окрестности V(p0), переходит в функцию Л. у. п. t, т. е.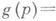 =
= Если V(p0).и V(p1 )-две отмеченные окрестности такие, что
Если V(p0).и V(p1 )-две отмеченные окрестности такие, что  tp0 и tp1 - соответствующие Л. у. п., то
tp0 и tp1 - соответствующие Л. у. п., то  есть однолистная голоморфная функция на нек-рой подобласти D(РО), осуществляющая биголоморфное отображение этой подобласти в D(р х).
есть однолистная голоморфная функция на нек-рой подобласти D(РО), осуществляющая биголоморфное отображение этой подобласти в D(р х).
Если R=RF - риманова поверхность аналитич. функции w=F(z).и р 0- регулярный элемент F(z) с проекцией 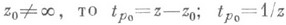 при
при  Если р 0- особый, или "алгебраический, элемент F(z), соответствующий ветвления точке z0 порядка k-1>0, то
Если р 0- особый, или "алгебраический, элемент F(z), соответствующий ветвления точке z0 порядка k-1>0, то  при
при 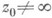 и
и  при
при 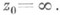 В отмеченной окрестности элемента р 0 Л. у. п. tфактически осуществляет при этом локальную униформизацию, вообще говоря, многозначного соотношения w=F(z).по формулам (для примера, при
В отмеченной окрестности элемента р 0 Л. у. п. tфактически осуществляет при этом локальную униформизацию, вообще говоря, многозначного соотношения w=F(z).по формулам (для примера, при 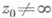 ):
):

В случае, когда R - риманова поверхность с краем, для точек р 0, принадлежащих краю R, Л. у. п.  отображает отмеченную окрестность V(p0) на полукруг
отображает отмеченную окрестность V(p0) на полукруг

Если R - риманова область над комплексным пространством 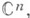 n>1, то Л. у. п. ,
n>1, то Л. у. п. ,

осуществляет гомеоморфное отображение отмеченной окрестности V(p0) на поликруг
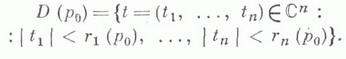
При этом, если пересечение  не пусто, то отображение
не пусто, то отображение  биголоморфно отображает нек-рую подобласть D(рД) в D(р х).
биголоморфно отображает нек-рую подобласть D(рД) в D(р х).
Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; [2] С п р и н г е р Д ж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [3] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976. Е. Д. Соломенцев.



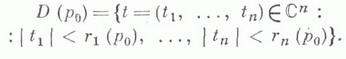

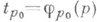 точки р римановой поверхности R всюду в нек-рой окрестности V(p0) точки
точки р римановой поверхности R всюду в нек-рой окрестности V(p0) точки  реализующая гомеоморфное отображение окрестности V(p0) на круг
реализующая гомеоморфное отображение окрестности V(p0) на круг  причем
причем  При этом V(p0) наз. отмеченной, или параметрической, окрестностью,
При этом V(p0) наз. отмеченной, или параметрической, окрестностью,
 - отмеченным, или параметрическим, отображением, D(р 0) - отмеченным, или параметрическим, к р у г о м. При отмеченном отображении любая функция точки g(p), определенная в отмеченной окрестности V(p0), переходит в функцию Л. у. п. t, т. е.
- отмеченным, или параметрическим, отображением, D(р 0) - отмеченным, или параметрическим, к р у г о м. При отмеченном отображении любая функция точки g(p), определенная в отмеченной окрестности V(p0), переходит в функцию Л. у. п. t, т. е.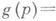 =
= Если V(p0).и V(p1 )-две отмеченные окрестности такие, что
Если V(p0).и V(p1 )-две отмеченные окрестности такие, что  tp0 и tp1 - соответствующие Л. у. п., то
tp0 и tp1 - соответствующие Л. у. п., то  есть однолистная голоморфная функция на нек-рой подобласти D(РО), осуществляющая биголоморфное отображение этой подобласти в D(р х).
есть однолистная голоморфная функция на нек-рой подобласти D(РО), осуществляющая биголоморфное отображение этой подобласти в D(р х).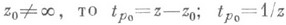 при
при  Если р 0- особый, или "алгебраический, элемент F(z), соответствующий ветвления точке z0 порядка k-1>0, то
Если р 0- особый, или "алгебраический, элемент F(z), соответствующий ветвления точке z0 порядка k-1>0, то  при
при 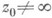 и
и  при
при 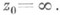 В отмеченной окрестности элемента р 0 Л. у. п. tфактически осуществляет при этом локальную униформизацию, вообще говоря, многозначного соотношения w=F(z).по формулам (для примера, при
В отмеченной окрестности элемента р 0 Л. у. п. tфактически осуществляет при этом локальную униформизацию, вообще говоря, многозначного соотношения w=F(z).по формулам (для примера, при 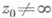 ):
): отображает отмеченную окрестность V(p0) на полукруг
отображает отмеченную окрестность V(p0) на полукруг 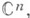 n>1, то Л. у. п. ,
n>1, то Л. у. п. , не пусто, то отображение
не пусто, то отображение  биголоморфно отображает нек-рую подобласть D(рД) в D(р х).
биголоморфно отображает нек-рую подобласть D(рД) в D(р х).