"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОКАЛЬНОЕ РАЗБИЕНИЕЗначение ЛОКАЛЬНОЕ РАЗБИЕНИЕ в математической энциклопедии:
- свойство расположения замкнутого множества Ф в пространстве 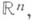 заключающееся в существовании такой точки а(точка, в к-рой множество Ф разбивает пространство) и такого положительного числа заключающееся в существовании такой точки а(точка, в к-рой множество Ф разбивает пространство) и такого положительного числа 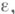 что при любом числе что при любом числе 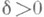 в открытом множестве в открытом множестве 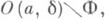 где где 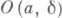 - (открытый) шар радиуса - (открытый) шар радиуса 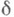 с центром а, содержится пара точек, обладающая свойством: всякий лежащий в с центром а, содержится пара точек, обладающая свойством: всякий лежащий в 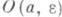 континуум, содержащий эту пару точек, имеет непустое пересечение с множеством Ф. К. Менгер (К. Menger) и П. С. Урысон доказали, что лежащее в плоскости замкнутое множество ф тогда и только тогда имеет размерность 1, когда оно не содержит внутренних (относительно плоскости) точек и локально разбивает плоскость (хотя бы в одной точке а). континуум, содержащий эту пару точек, имеет непустое пересечение с множеством Ф. К. Менгер (К. Menger) и П. С. Урысон доказали, что лежащее в плоскости замкнутое множество ф тогда и только тогда имеет размерность 1, когда оно не содержит внутренних (относительно плоскости) точек и локально разбивает плоскость (хотя бы в одной точке а).
Аналогичная характоризация замкнутых (n-1) -мерных множеств в re-мерном пространстве  дана П. С. Александровым (см. Локальное зацепление). дана П. С. Александровым (см. Локальное зацепление).
А. А. Мальцев.
|

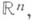 заключающееся в существовании такой точки а(точка, в к-рой множество Ф разбивает пространство) и такого положительного числа
заключающееся в существовании такой точки а(точка, в к-рой множество Ф разбивает пространство) и такого положительного числа 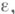 что при любом числе
что при любом числе 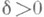 в открытом множестве
в открытом множестве 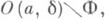 где
где 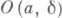 - (открытый) шар радиуса
- (открытый) шар радиуса 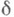 с центром а, содержится пара точек, обладающая свойством: всякий лежащий в
с центром а, содержится пара точек, обладающая свойством: всякий лежащий в 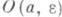 континуум, содержащий эту пару точек, имеет непустое пересечение с множеством Ф. К. Менгер (К. Menger) и П. С. Урысон доказали, что лежащее в плоскости замкнутое множество ф тогда и только тогда имеет размерность 1, когда оно не содержит внутренних (относительно плоскости) точек и локально разбивает плоскость (хотя бы в одной точке а).
континуум, содержащий эту пару точек, имеет непустое пересечение с множеством Ф. К. Менгер (К. Menger) и П. С. Урысон доказали, что лежащее в плоскости замкнутое множество ф тогда и только тогда имеет размерность 1, когда оно не содержит внутренних (относительно плоскости) точек и локально разбивает плоскость (хотя бы в одной точке а). дана П. С. Александровым (см. Локальное зацепление).
дана П. С. Александровым (см. Локальное зацепление).