" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА

Значение ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА в математической энциклопедии:

группа, каждая конечно порожденная подгруппа к-рой нильпотентна (см. Нильпотентная группа). В Л. н. г. все элементы конечного порядка образуют нормальную подгруппу, являющуюся периодич. частью этой группы. Эта подгруппа разлагается в прямое произведение силовских подгрупп, а факторгруппа по ней не имеет кручения. Л. н. г. без кручения обладает свойством однозначности извлечения корня: если для элементов аи bпри каком-либо целом 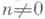будет а ^п=b ^п, то а=b. Каждая Л. н. г. Gбез кручения обладает Мальцев^ с к и м пополнением, т. е. вкладывается в однозначно определенную Л. н. г. без кручения G* такую, что в ней разрешимы все уравнения вида xⁿ = g, где 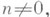a g - любой элемент из G. Это пополнение функториально, т. е. любой гомоморфизм 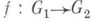Л. н. г. без кручения G₁ в G₂ однозначно продолжается до гомоморфизма

Лит.:[1] . К у р о ш А. Г., Теория групп, 3 изд., М., 1967; [2] Каргаполов М. И., Мерзляков Ю. И., Основы теории групп, 2 изд., М., 1977. А. Л. Шмелъкин.