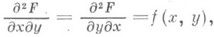" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЛОКАЛЬНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ

Значение ЛОКАЛЬНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ в математической энциклопедии:

в точке М - функция, интегрируемая в том или ином смысле в нек-рой окрестности точки М. Если действительная функция f, определенная на отрезке [ а, b], есть точная конечная производная функции F, действительной и определенной на том же отрезке, то f локально интегрируема по Лебегу в точках нек-рого открытого всюду плотного на [ а, b]множества. В двумерном случае (см. [2]) существует действительная функция f, определенная на квадрате являющаяся точной конечной повторной производной в любом порядке

к-рая не будет локально интегрируемой по Лебегу ни в одной точке квадрата.

Лит.:[1] Сакс С., Теория интеграла, пер. с англ., М., 1949; [2] Т о л с т о в Г. П., "Тр. Матем. ин-та АН СССР", 1950, т. 35, с. 1-101. И. А. Виноградова.