"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АРХИМЕДОВА ГРУППАЗначение АРХИМЕДОВА ГРУППА в математической энциклопедии:
- частично упорядоченная группа, в к-рой выполняется аксиома Архимеда: из того, что 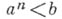 для всех целых ( для всех целых ( - элементы А. г.), следует, что а - единица группы (в аддитивной записи: из - элементы А. г.), следует, что а - единица группы (в аддитивной записи: из 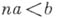 для всех целых пследует, что для всех целых пследует, что  ). Для линейно упорядоченных А. г. существует следующее описание (теорема Гёльдера): линейно упорядоченная группа тогда и только тогда архимедова, когда она изоморфна нек-рой подгруппе аддитивной группы действительных чисел с естественным порядком. Таким образом, аддитивная группа всех действительных чисел является, в нек-ром смысле, самой большой линейно упорядоченной А. г. Всякая линейно упорядоченная А. г. коммутативна. Линейно упорядоченная группа без нетривиальных выпуклых подгрупп - архимедова. ). Для линейно упорядоченных А. г. существует следующее описание (теорема Гёльдера): линейно упорядоченная группа тогда и только тогда архимедова, когда она изоморфна нек-рой подгруппе аддитивной группы действительных чисел с естественным порядком. Таким образом, аддитивная группа всех действительных чисел является, в нек-ром смысле, самой большой линейно упорядоченной А. г. Всякая линейно упорядоченная А. г. коммутативна. Линейно упорядоченная группа без нетривиальных выпуклых подгрупп - архимедова.
Лит.:[1] Биркгоф Г., Теория структур, пер. с англ., М., 1952; [2] Кокорин А. И., Копытов В. М., Линейно упорядоченные группы, М., 1972; [31 Фукс Л., Частично упорядоченные алгебраические системы, пер. с англ., М., 1965.
А. И. Кокорин, В. М. Копытов.
|

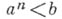 для всех целых (
для всех целых ( - элементы А. г.), следует, что а - единица группы (в аддитивной записи: из
- элементы А. г.), следует, что а - единица группы (в аддитивной записи: из 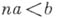 для всех целых пследует, что
для всех целых пследует, что  ). Для линейно упорядоченных А. г. существует следующее описание (теорема Гёльдера): линейно упорядоченная группа тогда и только тогда архимедова, когда она изоморфна нек-рой подгруппе аддитивной группы действительных чисел с естественным порядком. Таким образом, аддитивная группа всех действительных чисел является, в нек-ром смысле, самой большой линейно упорядоченной А. г. Всякая линейно упорядоченная А. г. коммутативна. Линейно упорядоченная группа без нетривиальных выпуклых подгрупп - архимедова.
). Для линейно упорядоченных А. г. существует следующее описание (теорема Гёльдера): линейно упорядоченная группа тогда и только тогда архимедова, когда она изоморфна нек-рой подгруппе аддитивной группы действительных чисел с естественным порядком. Таким образом, аддитивная группа всех действительных чисел является, в нек-ром смысле, самой большой линейно упорядоченной А. г. Всякая линейно упорядоченная А. г. коммутативна. Линейно упорядоченная группа без нетривиальных выпуклых подгрупп - архимедова.