|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОКАЛИЗАЦИЯЗначение ЛОКАЛИЗАЦИЯ в математической энциклопедии: в коммутативной алгебре - переход от коммутативного кольца Ак частных кольцу A[S-1], где S- нек-рое подмножество А. Кольцо A[S-1]можно определить как решение задачи об универсальном отображении Ав кольцо, при к-ром все элементы множества S становятся обратимыми. Имеются, однако, и явные конструкции А[S-1]: 1) как множества дробей вида a/s, где 2) как факторкольцо кольца многочленов A[Xs], 3) как индуктивный предел индуктивной системы A-модулей Кольцо Аканонически отображается в A[S-1]и превращает последнее кольцо в А-алгебру. Это отображение Без потери общности множество Sможно считать замкнутым относительно произведения (такое множество наз. мультипли кативным, или мультипликативной системой). В этом случае кольцо A[S-1]обозначается также S-1A или AS- Важнейшие примеры мультипликативных систем: а) множество {sn} всех степеней элементов б) множество в) множество Rвсех не делителей нуля в А. Кольцо R-1A наз. полным кольцом частных кольца А. Если Ацелостно, R-1A=A(0) является полем частных. Операция локализации без труда переносится на произвольные A-модули М, если положить  Переход от Мк М[S-1]является точным функтором. Иначе говоря, A-модуль A[S-1]является плоским. Л. коммутирует с прямыми суммами и индуктивными пределами. С геометрич. точки зрения Л. означает переход к открытому подмножеству. Точнее, для  На Л. можно смотреть как на операцию, позволяющую обратить морфизмы умножения на Лит.:[1] Б у р б а к и Н., Коммутативная алгебра, пер. С франц., М., 1971. В. И- Данилов. |
|
|
|
a s является произведением элементов из S(при этом две дроби a/s и a'/s' считаются эквивалентными тогда и только тогда, когда найдется s", являющийся произведением элементов из Sи такой, что 
складываются и умножаются дроби по обычным правилам);
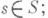по идеалу, порожденному многочленами 
где iпробегает естественно упорядоченный свободный коммутативный моноид N(s). При этом все А i изоморфны А, а гомоморфизмы 
->
совпадают с умножением на 
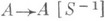инъективно тогда и только тогда, когда S не содержит ни одного делителя нуля в А, Напротив, если Sсодержит нильпотентный элемент, то A[S-1]=0.
то есть дополнение к простому идеалу 
Соответствующее кольцо частных является локальным и обозначается 
спектр Spec A[s-1]канонически отожествляется с открытым (в Зариского топологии).подмножеством 
состоящим из простых идеалов 
не содержащих s. Более того, эта операция позволяет связать с каждым A-модулем Мквазикогерентный пучок 
на аффинной схеме Spec A, для к-рого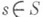 
в категории A-модулей. При таком подходе операция Л. допускает широкое обобщение на произвольные категории (см. Локализация в категориях).