|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛОГИКО-МАТЕМАТИЧЕСКИЕ ИСЧИСЛЕНИЯЗначение ЛОГИКО-МАТЕМАТИЧЕСКИЕ ИСЧИСЛЕНИЯ в математической энциклопедии: прикладные исчисления,- формализации математич. теорий. Л.-м. и. задается своим языком и перечнем постулатов (эти элементы образуют синтаксис).и в большинстве случаев снабжается семантикой. Существенными чертами, отличающими Л.-м. и. от аксиоматич. теорий традиционной математики, являются: 1) выявление используемых теорий логич. средств путем формулирования всех аксиом и вывода правил, позволяющих выводить одно суждение из другого; 2) переход от разговорного языка к точному формальному языку. Обычно Л.-м. и. строится на базе нек-рого логического исчисления (базисного логического исчисления). Язык Л.-м. и. получается из языка этого логич. исчисления добавлением символов специальных функций и предикатов (и, быть может, удалением предикатных переменных и переменных для функций). Перечень постулатов Л.-м. и. получается путем добавления к перечню постулатов базисного логич. исчисления (понимаемых применительно к новому языку) нек-рых постулатов, описывающих свойства добавленных функций и предикатов. Напр., язык элементарной теории групп получается по этой схеме из языка классич. исчисления предикатов с равенством: добавляются символы (умножение), inv (обращение) и е(единица), а выбрасываются все предикатные символы, кроме равенства. Дополнительный постулат  утверждает, что е - групповая единица, inv (x) - элемент, обратный к x, и умножение ассоциативно. Л.-м. <и., построенные на основе исчисления предикатов с равенством, служат для описания наиболее часто встречающихся математич. структур. Среди них арифметика формальная, формализованный анализ (с кванторами 1-го и 2-го порядков), аксиоматические теории множеств и т. д. Семантика Л.-м. и. задает интерпретацию переменных, математич. символов (символов предикатов и функций) и логич. операций. Этим определяются модели Л.-м. и. Из истинности формулы на любой модели, где истинны аксиомы нек-рого Л.-м. и., основанного на классич. исчислении предикатов с равенством, следует, в силу Гёделя теоремы о полноте, выводимость этой формулы в рассматриваемом Л.-м. и. Простейшими по своей структуре являются бескванторные Л.-м. и. Они употребляются чаще всего для описания свойств различных классов вычислимых функций. Язык бескванторного Л.-м. и. строится на основе языка исчисления высказываний с равенством или даже состоит из одних равенств. В первом случае логич. аппаратом Л.-м. и. служит классич. исчисление высказываний, во втором случае Л.-м. и. оформляется в виде исчисления равенств. Постулатами в обоих случаях считаются: 1) определяющие равенства рассматриваемых функций (напр., Предметные переменные ПРА (а),( аа), ( ааа), ...;функциональные переменные (f). (ff), (fff), . . .; натуральные числа 0, 0', 0", . . . Функциональные символы (функторы) строятся из исходных - ("следующий за"), Z (тождественный 0), [J, п, т]( т - местная функция, значение к-рой равно n-му аргументу), где n, т - натуральные числа,  Термы ПРА: 0, предметные переменные и выражения вида Формулы ПРА: r=s, где r, s - термы. Допустимые значения предметных переменных - натуральные числа, допустимые значения функциональных переменных - примитивно рекурсивные функции (иногда более широкие классы вычислимых функций). При описании частичных (не всюду определенных) функций, кроме предиката равенства, появляется предикат  Добавляется аксиома !t, где t - предметная переменная или константа, а также аксиомы вида  Употребляются также Л.-м. и. для описания вычислимых функционалов различных типов: 0 есть тип (объекты типа 0 - натуральные числа); если s и t - типы, то Важное свойство Л.-м. и. - дедуктивная полнота: она означает, что каждая формула без свободных переменных выводима или опровержима. Из дедуктивной полноты Л.-м. и. следует разрешимость проблемы выводимости - существование алгоритма, позволяющего по каждой формуле узнать, выводима она или нет. Примером дедуктивно полного Л.-м. и. является теория алгебраически замкнутых полей (система Тарского). Согласно Гёделя теореме о неполноте дедуктивно полные теории редки: всякое Л.-м. и., содержащее нек-рый весьма узкий фрагмент арифметики, дедуктивно неполно. Для еще более широкого класса Л.-м. и. проблема выводимости алгоритмически неразрешима. Важная характеристика Л.-м. и.- его выразительная способность. Часто удается ввести выразительные средства, не фигурирующие явно в языке рассматриваемого Л.-м. и. Так, в бескванторных языках удается ввести логич. связки и ограниченные кванторы:  В языке формальной арифметики можно говорить о конечных множествах, частично рекурсивных функциях и т. д. Одни логич. связки выражаются через другие; так, в исчислениях 2-го порядка (в том числе основанных на интуиционистской логике) все связки выражаются через Лит.:[1] Гильберт Д., Б е р н а й с П., Основания математики. Логические исчисления и формализация арифметики, пер. с нем., М., 1979; [2] Новиков П. С., Элементы математической логики, 2 изд., М., 1973; [3] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [4] Чёрч А., Введение в математическую логику, пер. с англ., т. 1, М., I960;. [5] Л и н до н Р., Заметки по логике, пер. с англ., М., 1968. Г. Е. Минц. |
|
|
|

 ), 2) основные свойства равенства, 3) рассуждения методом матемвтич. индукции (чаще всего по образцу "из
), 2) основные свойства равенства, 3) рассуждения методом матемвтич. индукции (чаще всего по образцу "из 
 ) можно вывести f(x) = g(x)"), 4) рассуждение, соответствующее
) можно вывести f(x) = g(x)"), 4) рассуждение, соответствующее  удалению: "из (х).вывести A(t)"(правило подстановки вместо свободной предметной переменной). Пример - система ПРА (примитивно рекурсивная арифметика).
удалению: "из (х).вывести A(t)"(правило подстановки вместо свободной предметной переменной). Пример - система ПРА (примитивно рекурсивная арифметика). с помощью подстановки ,9 и примитивной рекурсии R:если j есть га-местный функтор,
с помощью подстановки ,9 и примитивной рекурсии R:если j есть га-местный функтор,  суть m-местные функторы, то
суть m-местные функторы, то 
 (результат подстановки
(результат подстановки  ) есть m-местный функтор; если j есть re-местный функтор,
) есть m-местный функтор; если j есть re-местный функтор, есть (n+2) -местный функтор, то
есть (n+2) -местный функтор, то  есть (n+1) местнын функтор [примитивная рекурсия:
есть (n+1) местнын функтор [примитивная рекурсия: где s, s1 ..., sn - термы, j - функтор.
где s, s1 ..., sn - термы, j - функтор. или ! ("определено"); r=s интерпретируется в этом случае как
или ! ("определено"); r=s интерпретируется в этом случае как  и из !r следует, что значение r равно значению s". Добавляются также средства для изображения функции, универсальной для рассматриваемого класса: либо символ для этой функции, либо правило: если t - терм, то <t> - функтор (номер к-рого в нек-рой заранее фиксированной нумерации рассматриваемого класса равен t). Постулаты
и из !r следует, что значение r равно значению s". Добавляются также средства для изображения функции, универсальной для рассматриваемого класса: либо символ для этой функции, либо правило: если t - терм, то <t> - функтор (номер к-рого в нек-рой заранее фиксированной нумерации рассматриваемого класса равен t). Постулаты  -удаления и
-удаления и  -введения модифицируются:
-введения модифицируются: есть тип (операций, перерабатывающих объекты типа ав объекты типа t). Это - конечные типы (см. Типов теория). Рассматриваются также трансфинитные типы. Для каждого типа указываются переменные и константы этого типа, в их число обычно входит символ операции, все значения к-рой равны О, а также объект ' типа
есть тип (операций, перерабатывающих объекты типа ав объекты типа t). Это - конечные типы (см. Типов теория). Рассматриваются также трансфинитные типы. Для каждого типа указываются переменные и константы этого типа, в их число обычно входит символ операции, все значения к-рой равны О, а также объект ' типа  Для каждого sв число констант типа
Для каждого sв число констант типа  часто включают оператор примитивной рекурсии. Термами типа s наз. переменные и константы типа а, выражения вида r(s), где r - терм типа
часто включают оператор примитивной рекурсии. Термами типа s наз. переменные и константы типа а, выражения вида r(s), где r - терм типа  s - терм типа t, а также выражение вида
s - терм типа t, а также выражение вида  к-рое интерпретируется как обозначение функционала, перерабатывающего хв r(х), где rтипа b, хтипа a и
к-рое интерпретируется как обозначение функционала, перерабатывающего хв r(х), где rтипа b, хтипа a и  Бескванторные Л.-м. и. для функционалов конечных типов используются для математич. изучения кванторных Л.-м. и. В частности, с помощью бескванторной системы примитивно рекурсивных функционалов удается доказать непротиворечивость формальной арифметики; добавление оператора т. н. бар-рекурсии позволяет доказать непротиворечивость формализованного анализа.
Бескванторные Л.-м. и. для функционалов конечных типов используются для математич. изучения кванторных Л.-м. и. В частности, с помощью бескванторной системы примитивно рекурсивных функционалов удается доказать непротиворечивость формальной арифметики; добавление оператора т. н. бар-рекурсии позволяет доказать непротиворечивость формализованного анализа. напр.
напр.  эквивалентно
эквивалентно 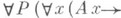
 Принципиальные ограничения выразительной способности языка дает теорема Тарского: при естественной нумерации формул языка, содержащего нек-рый минимум арифметики, невозможно указать формулу Т(х).этого языка такую, что Т(п).истинно тогда и только тогда, когда п - номер истинной формулы. Для Л.-м. и., основанных на конструктивной (интуиционистской) логике, часто имеет место теорема о "расщеплении" дизъюнкций: из выводимости замкнутой формулы
Принципиальные ограничения выразительной способности языка дает теорема Тарского: при естественной нумерации формул языка, содержащего нек-рый минимум арифметики, невозможно указать формулу Т(х).этого языка такую, что Т(п).истинно тогда и только тогда, когда п - номер истинной формулы. Для Л.-м. и., основанных на конструктивной (интуиционистской) логике, часто имеет место теорема о "расщеплении" дизъюнкций: из выводимости замкнутой формулы  следует выводимость одной из формул А, В. Для исследования структуры таких Л.-м. и. применяются различные аналоги понятия реализуемости. Вопросы непротиворечивости Л.-м. и., независимости отдельных постулатов, существования отделенных аксиоматик (т. е. таких, что каждая выводимая формула Аимеет вывод, использующий постулаты лишь для импликации и символов, входящих в А), существование интерпретаций одних Л.-м. и. в других исследуются в доказательств теории.
следует выводимость одной из формул А, В. Для исследования структуры таких Л.-м. и. применяются различные аналоги понятия реализуемости. Вопросы непротиворечивости Л.-м. и., независимости отдельных постулатов, существования отделенных аксиоматик (т. е. таких, что каждая выводимая формула Аимеет вывод, использующий постулаты лишь для импликации и символов, входящих в А), существование интерпретаций одних Л.-м. и. в других исследуются в доказательств теории.