|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ ГРУПП АРИФМЕТИЧЕСКАЯ ТЕОРИЯЗначение ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ ГРУПП АРИФМЕТИЧЕСКАЯ ТЕОРИЯ в математической энциклопедии: - теория, изучающая арифметич. свойства линейных алгебраических групп, определенных, как правило, над глобальным полем. Одним из главных объектов изучения Л. а. г. а. т. являются арифметич. подгруппы алгебраич. группы G(см. Арифметическая группа), а одним из основных технич. инструментов - группа аделей С A. На GA можно определить нек-рым естественным образом меру, наз. Тамагавы мерой. Один из первых возникающих здесь вопросов: когда объем факторпространства группы GA по подгруппе главных аделей GA конечен? Полный ответ на него был получен А. Борелем (А. Воrel). Оказалось, напр., что объем Используя теорию приведения для подгрупп главных аделей, удалось во многих случаях вычислить объем Во всех основных вопросах Л. а. г. а. т. существенную роль играют теоремы аппроксимации, редуцирующие исследование арифметич. свойств алгебраич. групп, определенных над глобальными полями к исследованию арифметич. свойств алгебраич. групп, определенных над локальными полями. Наибольшее значение имеет проблема сильной аппроксимации (п. с. а.) в алгебраич. группах, к-рая состоит в следующем. Пусть V={v} - множество всех неэквивалентных нормировании поля k; kv - пополнение kотносительно v; Ov - кольцо целых элементов  где  для  М. Эйхлер [13] решил проблему сильной аппроксимации для групп SL(n, D), где D - тело конечного k-ранга. Позднее различные частные случаи этой проблемы исследовали М. Кнезер (М. Kneser), Г. Шимура (G. Shimura), А. Вейль (A. Well, см. [4]). Проблема сильной аппроксимации была решена (см. [9], [10]) для классич. групп над числовыми полями и найдены необходимые условия для ее положительного решения в общем случае; а именно: а) группа Gдолжна быть односвязной как алгебраич. группа и б) если F - любая простая компонента полупростой части G, то группа FS должна быть некомпактной. Необходимость этих условий доказана [14] для функционального поля. Наконец, была доказана [7] (см. также [16]) достаточность условий а) и б) как над числовыми, так и над функциональными полями, что дало полное решение п. с. а. В основе метода доказательства лежит редукция п. с. а. к доказательству Кнезера - Титса гипотезы о строении односвязных групп над локальными полями: если Gесть kv -простая односвязная kv -изотропная группа, то  это показывает, что арифметика G0 в значительной степени определяется арифметикой локальных компонент Наряду с сильной аппроксимацией существенную роль в Л. а. г. а. т. играет свойство слабой аппроксимации (с. с. а.) алгебраич. группы G относительно S, к-рое состоит в том, что образ G л, при канонич. проекции Важную роль в Л. а. г. а. т. играют когомологич. методы, в частности принцип Хассе (см. Галуа когомологии). Лит.:[1] Арифметические группы и автоморфные функции, пер. с англ. и франц., М., 1969; [2] Алгебраическая теория чисел, пер. с англ., М., 1969; [3] Вейль А., Основы теории чисел, пер. с англ., М., 1972; [4] его же, "Математика", 1969, т. 13, № 6, с. 18-98; [5] Борель А., "Математика", 1964, т. 8, № 2, с. 3-17; [6] Б о р е л ь А., -X а р и ш - Ч а н д р а, "Математика", 1964, т. 8, № 2, с. 19-71; [7] Платонов В. П., "Изв. АН СССР. Сер. матем.", 1969, т. 33, № 6, с. 1211 - 19; 1970, т. 34, № 4, с. 775-77; [8] его ж е, "Труды Матем. ин-та АН СССР", 1973, т. 132, с. 102-68; [9] Kneser M., "J. reine und angew. Math.", 1965, Bd 218, S. 190-203; [10] его же, "Proc. Symp. Pure Math.", 1966, v. 9, p. 187-96; [11] его же, "Colloq. groupes algebriqus. Bruxelles", 1962, p. 41-52; [12] Harder G., "Inventiones Math.", 1967, v. 4, № 3, p. 165-91; [13] E i с h l е r М., "J. reine und angew. Math.", 1938, Bd 179, S. 227-51; [14] Вehr H., "J. reine und angew. Math.", 1968, Bd 229, S. 107 - 16; [15] Платонов В. П., "Труды Матем. ин-та АН СССР", 1976, т. 142, с. 198-207; [16] Р r a s a d G., "Ann. Math.", 1977, v. 105, p. 553 - 72. В. П. Платонов. |
|
|
|

 всегда конечен для полупростой группы. Решению этого вопроса предшествовало построение теории приведения для арифметич. групп (см. [5], [6]).
всегда конечен для полупростой группы. Решению этого вопроса предшествовало построение теории приведения для арифметич. групп (см. [5], [6]).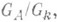 к-рый наз. числом Тамагавы группы G. Напр., для ортогональной группы G число Тамагавы F(G) = 2, и это фактически эквивалентно основному результату аналитич. теории квадратичных форм (см. [1]). Изучение структуры арифметич. групп (начатое в [6]) было продолжено затем в разных направлениях. Прежде всего следует отметить исследования по конгруэнц-проблеме, по проблеме максимальности арифметич. подгрупп и проблеме рода в арифметич. группах.
к-рый наз. числом Тамагавы группы G. Напр., для ортогональной группы G число Тамагавы F(G) = 2, и это фактически эквивалентно основному результату аналитич. теории квадратичных форм (см. [1]). Изучение структуры арифметич. групп (начатое в [6]) было продолжено затем в разных направлениях. Прежде всего следует отметить исследования по конгруэнц-проблеме, по проблеме максимальности арифметич. подгрупп и проблеме рода в арифметич. группах. - максимальный идеал Ov. Для произвольного конечного подмножества
- максимальный идеал Ov. Для произвольного конечного подмножества  через GS обозначается подгруппа в GA; у к-рой все v-компоненты при
через GS обозначается подгруппа в GA; у к-рой все v-компоненты при  равны единице. Спрашивается: когда
равны единице. Спрашивается: когда  (Здесь черта означает замыкание в топологии GA.).Если
(Здесь черта означает замыкание в топологии GA.).Если  (
( - множество всех архимедовых нормировании k), то эквивалентная формулировка этой проблемы: когда для любых
- множество всех архимедовых нормировании k), то эквивалентная формулировка этой проблемы: когда для любых 
 любых
любых  и положительных целых
и положительных целых  имеет решение в группе Gk система сравнений
имеет решение в группе Gk система сравнений  порождается унипотентными элементами или, эквивалентно, факторгруппа группы
порождается унипотентными элементами или, эквивалентно, факторгруппа группы  по ее центру проста в абстрактном смысле. В качестве простейшего применения сильной аппроксимационной теоремы получается следующий факт: пусть Gобладает свойством сильной аппроксимации относительно
по ее центру проста в абстрактном смысле. В качестве простейшего применения сильной аппроксимационной теоремы получается следующий факт: пусть Gобладает свойством сильной аппроксимации относительно  если О - кольцо целых элементов k, то
если О - кольцо целых элементов k, то 
 плотен в GS. Все односвязные группы обладают с. с. а. С другой стороны, имеются примеры полупростых групп и алгебраич. торов, не обладающих с. с. а. (см. [11], [2]). Тем не менее для широкого класса неодносвязных полупростых групп, в частности для присоединенных групп, выполнено с. с. а. [12]. Если G - алгебраич. тор и для всякого
плотен в GS. Все односвязные группы обладают с. с. а. С другой стороны, имеются примеры полупростых групп и алгебраич. торов, не обладающих с. с. а. (см. [11], [2]). Тем не менее для широкого класса неодносвязных полупростых групп, в частности для присоединенных групп, выполнено с. с. а. [12]. Если G - алгебраич. тор и для всякого  тор G разложим над циклич. расширением поля kv, то G обладает с. с. а. относительно S. В нек-рых случаях с. с. а. выполнено для алгебраич. групп над произвольным полем (см. [11]). Существовала гипотеза (см. [11]), что с. с. а. выполнено для группы SL (n, D), где D - тело конечного k-ранга над произвольным бесконечным полем k. Однако развитие приведенной K-теории привело к отрицательному ответу (см. [15]): для группы SL(n, D).отклонение от слабой аппроксимации может быть сколь угодно большим.
тор G разложим над циклич. расширением поля kv, то G обладает с. с. а. относительно S. В нек-рых случаях с. с. а. выполнено для алгебраич. групп над произвольным полем (см. [11]). Существовала гипотеза (см. [11]), что с. с. а. выполнено для группы SL (n, D), где D - тело конечного k-ранга над произвольным бесконечным полем k. Однако развитие приведенной K-теории привело к отрицательному ответу (см. [15]): для группы SL(n, D).отклонение от слабой аппроксимации может быть сколь угодно большим.