|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕЗначение ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕ в математической энциклопедии: - уравнение вида  где A0(t), A1(t).при каждом t - линейные операторы в банаховом пространстве Е, g(t) - заданная, a u(t) - искомая функции со значениями в Е;производная ипонимается как предел по норме Еразностного отношения. 1. Линейное дифференциальное уравнение с ограниченным оператором. Пусть A0(t).и A1(t).при каждом t- ограниченные операторы, действующие в Е. Если оператор A0(t).имеет при каждом tограниченный обратный, то уравнение (1) разрешается относительно производной и принимает вид  где A(t) - ограниченный оператор в пространстве Е, f(t).и u(t) - функции со значениями в Е. Если функции A(t).и f(t).непрерывны (или, более общо, изме- римы и интегрируемы на каждом конечном промежутке), то решение задачи Коши:  существует при любом  где  - эволюционный оператор уравнения и=А(t)u. Решение задачи Коши для уравнения (2) определяется по формуле:  Из (4) вытекает оценка  ее уточнение  где  - спектральный радиус оператора - спектральный радиус оператора  Эволюционный оператор обладает свойствами  Основное внимание при изучении уравнения (2) уделяется поведению его решений на бесконечности в зависимости от поведения A(t).и f(t). При этом важной характеристикой уравнения является генеральный (или особый) показатель  Детально изучены уравнения с периодическими и почти периодическими коэффициентами (см. Качественная теория дифференциальных уравнений в банаховом пространстве). Уравнение (2) можно рассматривать и в комплексной плоскости. Если функции A(t).и f(t).голоморфны в односвязной области, содержащей точку s, то формулы (3), (4), (5), (5') остаются в силе, если под интегралами понимать интегралы по спрямляемому пути, соединяющему s и t. Ряд других вопросов возникает в случае, когда исходное линейное уравнение неразрешимо относительно производной. Если оператор A0(t).ограниченно обратим всюду, за исключением одной точки, напр. t=0, то уравнение в пространстве Еприводится к виду  где a(t).- скалярная функция и а(0)=0. Здесь основное внимание уделяется изучению поведения решений в окрестности нуля, при этом различаются аналитический и неаналитический случаи. Аналитический случай. Для простейшего уравнения 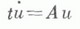 с постоянным оператором Аэволюционный оператор U(t)=U(t,0) имеет вид  решения неоднозначны: при обходе вокруг нуля в положительном направлении они умножаются на оператор Если для уравнения о регулярной особенностью  где ряд справа сходится в окрестности нуля, оператор U(t)искать в виде ряда  то для определения коэффициентов  Для разрешимости этой системы, т. е. формальной разрешимости уравнения (7), достаточно, чтобы спектры операторов A(0) и А (0)-kl не пересекались или, что то же, чтобы в спектре оператора A(0) не было точек, отличающихся на целое число. При этом условии ряд  сходится в той же окрестности нуля, что и ряд для A(t). Если теперь имеется конечное число целых чисел, представимых в виде разностей точек спектра оператора A(0), и каждое из них является изолированной точкой спектра трансформатора 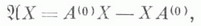 то существует решение вида  где Uk - целые функции аргумента lnt, удовлетворяющие при каждом  Если целые точки спектра трансформатора В случае иррегулярной особенности рассмотрено дифференциальное уравнение  в банаховой алгебре Неаналитический случай. Пусть в уравнении  функции A(t).и f (t).бесконечно дифференцируемы. В конечномерном случае получен исчерпывающий результат; если уравнение имеет формальное решение в виде степенного ряда, то оно имеет бесконечно дифференцируемое на [0, Т]решение, для к-рого формальный ряд является рядом Тейлора в точке t=0. В бесконечномерном случае имеется лишь ряд достаточных условий для существования бесконечно дифференцируемых решений. Пусть Пусть m=1. Если отрицательные целые числа не принадлежат спектру оператора А(0), то существует единственное бесконечно дифференцируемое решение. В аналогичных предположениях относительно оператора А(0) рассмотрены уравнения вида (6), в к-рых a(t).и f(t).имеют конечную гладкость и такой же гладкостью обладают решения. Своеобразная картина возникает, когда дифференциальное уравнение неразрешимо относительно производной при всех t, напр. когда А - постоянный необратимый оператор. Пусть в уравнении  операторы Аи В - ограниченные в пространстве Е, оператор Анеобратим и фредгольмов. Предполагается, что оператор Если оператор 2. Линейное дифференциальное уравнение с неограниченным оператором. Пусть A0(t).обратим при каждом t, так что уравнение (1) разрешается относительно производной и принимает вид  и пусть здесь A(t) - неограниченный оператор в пространстве Е с плотной в Еобластью определения D(A(t)), имеющий непустое резольвентное множество, f(t) - заданная, a u(t) - искомая функции со значениями в Е. Даже для простейшего уравнения u = Au с неограниченным оператором решения задачи Коши u(0) = u0 могут не существовать, могут быть неединственными, могут быть непродолжимыми на всю полуось, поэтому основные исследования посвящены вопросам существования и единственности решений. Под решением уравнения u = Au на отрезке [0, Т]понимается функция, принимающая значения в D(А), дифференцируемая на [0, Т]и удовлетворяющая уравнению. Иногда это определение является слишком жестким и вводится понятие ослабленного решения, как функции, обладающей теми же свойствами на (0, Т], а в точке 0 лишь непрерывной. Пусть оператор Аимеет резольвенту 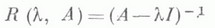 при всех достаточно больших положительных Тогда ослабленное решение задачи  единственно на отрезке [О, Т-h]и может разветвляться при t= Т-h. Если h = 0, то решение единственно на всей полуоси. В смысле поведения Если при каждом  при всех  При выполнении условий (11) этими свойствами обладают операторы Другой метод построения решений уравнения и = Аи основан на преобразовании Лапласа. Если резольвента оператора Аопределена на нек-ром контуре Г, то функция  формально удовлетворяет уравнению  Если обеспечить сходимость интегралов, законность дифференцирования под знаком интеграла и обращения в нуль последнего интеграла, то u(t).будет удовлетворять уравнению. Трудность состоит в том, что норма резольвенты не может на бесконечности убывать быстрее, чем  при достаточно больших  (слабо гиперболич. уравнение), и Г - граница этой области, получается решение лишь для u0. принадлежащих пересечению областей определения всех степеней оператора А, с определенным поведением Значительно больше ослабленных решений получается в том случае, когда Г уходит в левую полуплоскость и можно использовать убывание на нем функции Существование резольвенты на контурах, уходящих в левую полуплоскость, можно, пользуясь разложением в ряд, получить из соответствующих оценок на вертикальных прямых. Если при  то для каждого 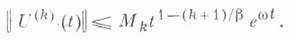 Если оценка (13) выполнена при Уравнение и=Аи наз. абстрактным параболическим, если существует единственное ослабленное решение на  то уравнение является абстрактным параболическим. Все его обобщенные решения аналитичны в нек-ром секторе, содержащем положительную полуось, и справедливо неравенство  где Сне зависит от и 0. Обратно, если уравнение обладает перечисленными свойствами, то для оператора Авыполнено (14). Если задача (10) имеет единственное ослабленное решение при любом 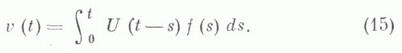 Функция v(t).определена при любой непрерывной f(t), поэтому она наз. обобщенным решением неоднородного уравнения. Для того чтобы обеспечить ее дифференцируемость, на функцию f(t) налагаются условия гладкости, и тем "больше", чем "хуже" полугруппа U(t). Так, в предыдущих условиях (15) будет ослабленным решением неоднородного уравнения, если f(t).дважды непрерывно дифференцируема; если выполнено (И), то (15) будет решением, если f(t) непрерывно дифференцируема; если выполнено (13) при  имеется несколько основных теорем существования и единственности решений (ослабленных решений) задачи Коши u(s) = u0 на отрезке  оператор A(t)сильно непрерывен по tна D(А) и  при  где U(t, s) - эволюционный оператор со свойствами: 1) U(t, s )сильно непрерывен в треугольнике   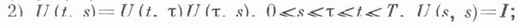 3) U(t, s).отображает D(А).в себя и оператор  ограничен и сильно непрерывен в 4) на D(А).оператор U(t, s).сильно дифференцируем по tи sи  Конструирование оператора U(t, s).проводится путем аппроксимации оператора A(t).ограниченными операторами An(t).и заменой последних кусочно постоянными операторами. Предыдущие условия на оператор A(t).во многих важных задачах не выполняются. Пусть для оператора A(t).существуют такие константы Ми w, что  для всех  Пусть в пространстве Еплотно вложено банахово пространство F, содержащееся во всех D(A(t)), и обладающее свойствами: а) оператор A(t).ограниченно действует из Fв Еи непрерывен по tпо норме ограниченных операторов из Fв Е; б).существует изоморфизм Sпространства Fна пространство Етакой, что 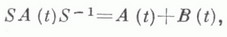 где В(t) - ограниченная в Есильно измеримая операторная функция, для к-рой ||В(t)||II интегрируема на [0, Т]. Тогда существует эволюционный оператор U(t, s), обладающий свойствами и U(t, s).сильно непрерывен в Fна Еи В теории параболич. уравнений применяется метод замороженных коэффициентов. Предполагается, что при каждом и = А(t0 )иотвечает полугрупповой оператор  В условиях, когда ядра этих уравнений имеют слабые особенности, доказывается существование их решения и то, что U(t, s).является эволюционным оператором. Наибольшие приложения нашло утверждение: если  при  и  (условие Гёльдера), то существует эволюционный оператор U(t, s), дающий при каждом Предположение о постоянстве D(A(t)).не позволяет в приложениях рассматривать краевые задачи с граничными условиями, зависящими от t. Пусть выполнено  в секторе Оператор U(t, s )для уравнения (16) формально удовлетворяет интегральному уравнению  В силу неограниченности оператора A(t).это уравнение нельзя решить методом последовательных приближений. Пусть имеется семейство банаховых пространств 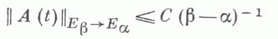 и A(t).непрерывен по tпо норме пространства ограниченных операторов из  В различных случаях при той или иной гладкости f(t).эта формула допускает обоснование. Лит.:[1] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [2] К р е й н С. Г., Линейные дифференциальные уравнения в банаховом пространстве, М., 1967; [3] Хилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [4] Функциональный анализ, 2 изд., М., 1972; [5] Г л у ш к о В. П., Линейные вырождающиеся дифференциальные уравнения, Воронеж, 1972; [6] Далецкий Ю. Л., Крейн М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970: [7] Зубова С. П., Чернышев К. И., в кн.: "Дифференциальные уравнения и их применения", Вильнюс, 1976, в. 14, с. 21-39; [8] Кузнецов А. Н., "Функциональный анализ и его прилож. ", 1972, т. 6, № 2, с. 41-51; [9] К р е й н С. Г., Лаптев Г. И., "Дифференциальные уравнения", 1969, т. 5, М 8, с. 1458-69; [101 Л ю б и ч Ю. И., "Успехи матем. наук", 1966, т. 21, в. 3, с. 3-51; [11] Овеянников Л. В., "Докл. АН СССР", 1965, т. 163, № 4, с. 819- -822; [12] Соболевский П. Е., "Тр. Моск. матем. об-ва", 196), т. 10, с. 297-350; [13] Beals R., в кн.: Ргос. NATO Adv. Study Inst., Lifcge, 1976, p. 1-26; [14] P r i e d m a n A., "Arch. Rat. Mech. and Anal.", 1964, v. 17, №5 5, p. 353-57; [15] К a to Т., "J. Math. Soc. Japan", 1973, v. 25, №4, p. 648-66: [16] Treve s F., Basic linear partial differential equations, N. Y., 1975; [17] Miller J., "Acta math.", 1963, V. 110, №3-4, p. 209-31. С. Г. Крейн. |
|
|
|

 и задается формулой
и задается формулой 
 получается система уравнений
получается система уравнений  условию
условию  являются полюсами его резольвенты, то функции Uk - многочлены.
являются полюсами его резольвенты, то функции Uk - многочлены. (напр., в алгебре ограниченных операторов в банаховом пространстве Е). При нек-рых ограничениях на оператор A(0) оно с помощью интегралов Лапласа сводится к уравнению с регулярной особенностью (m=1) в алгебре матриц с элементами из алгебры
(напр., в алгебре ограниченных операторов в банаховом пространстве Е). При нек-рых ограничениях на оператор A(0) оно с помощью интегралов Лапласа сводится к уравнению с регулярной особенностью (m=1) в алгебре матриц с элементами из алгебры 
 Если спектр оператора А(0) не пересекается с мнимой осью, то существует семейство бесконечно дифференцируемых решений, зависящее от произвольного элемента g-, принадлежащего инвариантному подпространству оператора А(0), отвечающему части спектра А(0), лежащей в левой полуплоскости. Любое непрерывное на [О, Т]решение входит в это семейство. Если весь спектр А(0) лежит в левой полуплоскости, то существует только одно бесконечно дифференцируемое решение.
Если спектр оператора А(0) не пересекается с мнимой осью, то существует семейство бесконечно дифференцируемых решений, зависящее от произвольного элемента g-, принадлежащего инвариантному подпространству оператора А(0), отвечающему части спектра А(0), лежащей в левой полуплоскости. Любое непрерывное на [О, Т]решение входит в это семейство. Если весь спектр А(0) лежит в левой полуплоскости, то существует только одно бесконечно дифференцируемое решение. непрерывно обратим при достаточно малых e. Тогда существуют такие разложения в прямые суммы
непрерывно обратим при достаточно малых e. Тогда существуют такие разложения в прямые суммы  и
и  что операторы Аи Вотображают
что операторы Аи Вотображают  в M(2). Оператор Аобратим на M(1) и отображает на M(2). Подпространство N(1) конечномерно. Все решения уравнения (8) лежат в подпространстве M(1) и имеют вид
в M(2). Оператор Аобратим на M(1) и отображает на M(2). Подпространство N(1) конечномерно. Все решения уравнения (8) лежат в подпространстве M(1) и имеют вид  где
где  - сужение Ана M(1),
- сужение Ана M(1),  _ Для неоднородного уравнения Аи=Bu+f(t).решение существует только при определенной гладкости f(t) и нек-рых условиях согласования значений f(t).и ее производных с начальными данными. Количество производных, к-рые должны иметь нек-рые компоненты f(t), и количество условий согласования равны максимальной длине B-присоединенных цепочек оператора А. При выполнении указанных условий решение задачи Коши единственно.
_ Для неоднородного уравнения Аи=Bu+f(t).решение существует только при определенной гладкости f(t) и нек-рых условиях согласования значений f(t).и ее производных с начальными данными. Количество производных, к-рые должны иметь нек-рые компоненты f(t), и количество условий согласования равны максимальной длине B-присоединенных цепочек оператора А. При выполнении указанных условий решение задачи Коши единственно. необратим при всех
необратим при всех  то все решения уравнения (8) лежат в подпространстве, имеющем, вообще говоря, бесконечный дефект. Решение задачи Коши для него будет неединственным. От функции f(t)в неоднородном уравнении требуется бесконечное число условий дифференцируемости и условий согласования.
то все решения уравнения (8) лежат в подпространстве, имеющем, вообще говоря, бесконечный дефект. Решение задачи Коши для него будет неединственным. От функции f(t)в неоднородном уравнении требуется бесконечное число условий дифференцируемости и условий согласования. и
и 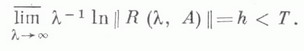
 при
при  это утверждение является точным.
это утверждение является точным. существует единственное непрерывно дифференцируемое на [О, Т]решение задачи (10), то это решение продолжается на всю полуось и представимо в виде
существует единственное непрерывно дифференцируемое на [О, Т]решение задачи (10), то это решение продолжается на всю полуось и представимо в виде  где U(t) - сильно непрерывная на
где U(t) - сильно непрерывная на  полугруппа ограниченных операторов, U(0)=I, для к-рой справедлива оценка
полугруппа ограниченных операторов, U(0)=I, для к-рой справедлива оценка  Для того чтобы уравнение обладало таким свойством, необходимо и достаточно, чтобы выполнялись неравенства
Для того чтобы уравнение обладало таким свойством, необходимо и достаточно, чтобы выполнялись неравенства  и m=1, 2, . . ., где Мне зависит от
и m=1, 2, . . ., где Мне зависит от  и т. Эти условия трудно проверяемы. Они выполнены, если
и т. Эти условия трудно проверяемы. Они выполнены, если  и тогда
и тогда  Если еще w=0, то U(t) - полугруппа сжатий. Это будет тогда и только тогда, когда А - максимальный диссипатиеный оператор. При
Если еще w=0, то U(t) - полугруппа сжатий. Это будет тогда и только тогда, когда А - максимальный диссипатиеный оператор. При  функция U(t)u0 не будет дифференцируемой (во всяком случае при t=0), ее часто наз. обобщенным решением уравнения (10). Решения уравнения и=Аи можно строить как предел при
функция U(t)u0 не будет дифференцируемой (во всяком случае при t=0), ее часто наз. обобщенным решением уравнения (10). Решения уравнения и=Аи можно строить как предел при 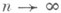 решений уравнений и = А n и с ограниченными операторами при тех же начальных условиях. Для этого достаточно, чтобы операторы А п коммутировали, сильно сходились к Ана D(А).и
решений уравнений и = А n и с ограниченными операторами при тех же начальных условиях. Для этого достаточно, чтобы операторы А п коммутировали, сильно сходились к Ана D(А).и  (операторы И о с и д ы).
(операторы И о с и д ы). Однако на нек-рых элементах она убывает быстрее. Напр., если
Однако на нек-рых элементах она убывает быстрее. Напр., если  определена при
определена при  и
и  то для
то для  формула (12) дает решение для любого
формула (12) дает решение для любого  В более "плохом" случае, когда предыдущее неравенство выполнено лишь в области
В более "плохом" случае, когда предыдущее неравенство выполнено лишь в области  при
при 
 При этом, как правило, решения обладают повышенной гладкостью при t>0. Если резольвента ограничена на контуре
При этом, как правило, решения обладают повышенной гладкостью при t>0. Если резольвента ограничена на контуре  где
где 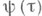 - гладкая неубывающая вогнутая функция, растущая на
- гладкая неубывающая вогнутая функция, растущая на  как
как  то функция (12) при любом
то функция (12) при любом  становится дифференцируемой и удовлетворяет уравнению, начиная с нек-рого t0, с дальнейшим увеличением tее гладкость повышается. Если
становится дифференцируемой и удовлетворяет уравнению, начиная с нек-рого t0, с дальнейшим увеличением tее гладкость повышается. Если  растет как степень
растет как степень  с показателем, меньшим единицы, то функция (12) бесконечно дифференцируема при t>0; если
с показателем, меньшим единицы, то функция (12) бесконечно дифференцируема при t>0; если  растет как
растет как  то u(t).принадлежит квази-аналитич. классу функций; если растет как линейная функция, то и(t) - аналитична. Во всех этих случаях она удовлетворяет уравнению и = Аи.
то u(t).принадлежит квази-аналитич. классу функций; если растет как линейная функция, то и(t) - аналитична. Во всех этих случаях она удовлетворяет уравнению и = Аи.
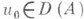 существует решение задачи (10). Все эти решения бесконечно дифференцируемы при t>0. Они представляются в виде u(t)=U(t)un, где U(t) - бесконечно дифференцируемая полугруппа при t>0, имеющая, вообще говоря, особенность при = 0. Для ее производных справедливы оценки
существует решение задачи (10). Все эти решения бесконечно дифференцируемы при t>0. Они представляются в виде u(t)=U(t)un, где U(t) - бесконечно дифференцируемая полугруппа при t>0, имеющая, вообще говоря, особенность при = 0. Для ее производных справедливы оценки  то все обобщенные решения уравнения и=Аи аналитичны в нек-ром секторе, содержащем положительную полуось.
то все обобщенные решения уравнения и=Аи аналитичны в нек-ром секторе, содержащем положительную полуось. удовлетворяющее начальному условию и(0) = и 0 при любом
удовлетворяющее начальному условию и(0) = и 0 при любом  Если
Если  производная к-рого суммируема на каждом конечном интервале, то эти решения представимы в виде u(t)= U(t)u0, где U(t).- сильно непрерывная полугруппа на
производная к-рого суммируема на каждом конечном интервале, то эти решения представимы в виде u(t)= U(t)u0, где U(t).- сильно непрерывная полугруппа на  а всякое ослабленное решение неоднородного уравнения v=Av+f(t).с нулевым начальным условием u(0)=u0 представимо в виде
а всякое ослабленное решение неоднородного уравнения v=Av+f(t).с нулевым начальным условием u(0)=u0 представимо в виде  то v(t).будет ослабленным решением, если f(t).удовлетворяет условию Гёльдера с показателем
то v(t).будет ослабленным решением, если f(t).удовлетворяет условию Гёльдера с показателем 
 Вместо гладкости f(t)).пo tможно требовать принадлежность значений f(t).области определения соответствующей степени оператора А. Для уравнения с переменным оператором
Вместо гладкости f(t)).пo tможно требовать принадлежность значений f(t).области определения соответствующей степени оператора А. Для уравнения с переменным оператором  Если область определения A(t).не зависит от t:
Если область определения A(t).не зависит от t: то решение задачи Коши единственно. Если, кроме того, A(t).сильно непрерывно дифференцируем на D(А), то при всяком
то решение задачи Коши единственно. Если, кроме того, A(t).сильно непрерывно дифференцируем на D(А), то при всяком  решение существует и представимо в виде
решение существует и представимо в виде 

 4') на Fоператор U(t, s).сильно дифференцируем в смысле нормы
4') на Fоператор U(t, s).сильно дифференцируем в смысле нормы  Сформулированное утверждение позволило получить теоремы существования для основных квазилинейных уравнений математич. физики гиперболич. типа.
Сформулированное утверждение позволило получить теоремы существования для основных квазилинейных уравнений математич. физики гиперболич. типа. уравнению
уравнению  Искомый эволюционный оператор формально удовлетворяет интегральным уравнениям
Искомый эволюционный оператор формально удовлетворяет интегральным уравнениям  ослабленное решение
ослабленное решение  задачи Коши. Единственность решения имеется при условии лишь непрерывности оператора
задачи Коши. Единственность решения имеется при условии лишь непрерывности оператора  (в гильбертовом пространстве). Теорема существования, аналогичная приведенной выше, справедлива для оператора A(t).с условием типа (13) при определенном соотношении между
(в гильбертовом пространстве). Теорема существования, аналогичная приведенной выше, справедлива для оператора A(t).с условием типа (13) при определенном соотношении между  и
и 
 тогда существует эволюционный оператор U(t, s). Здесь постоянство D(A(t)).не предполагается. Имеется вариант последнего утверждения, приспособленный к рассмотрению параболич. задач в нецилиндрич. областях, в к-ром D(A(t)).при каждом tлежит в нек-ром подпространстве Е(t).пространства Е.
тогда существует эволюционный оператор U(t, s). Здесь постоянство D(A(t)).не предполагается. Имеется вариант последнего утверждения, приспособленный к рассмотрению параболич. задач в нецилиндрич. областях, в к-ром D(A(t)).при каждом tлежит в нек-ром подпространстве Е(t).пространства Е. обладающее свойством:
обладающее свойством:  и
и  при
при  Предполагается, что оператор A(t).ограничен как оператор из
Предполагается, что оператор A(t).ограничен как оператор из 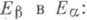
 Тогда в этом пространстве метод последовательных приближений для уравнения (17) будет сходиться при
Тогда в этом пространстве метод последовательных приближений для уравнения (17) будет сходиться при  Таким образом локально строится оператор U(i, s).как ограниченный оператор из Eb в Е a. В приложениях этот подход дает теоремы типа Коши - Ковалевской. Для неоднородного уравнения (9) при известном эволюционном операторе для уравнения и = А(t)uрешение задачи Коши формально записывается в виде
Таким образом локально строится оператор U(i, s).как ограниченный оператор из Eb в Е a. В приложениях этот подход дает теоремы типа Коши - Ковалевской. Для неоднородного уравнения (9) при известном эволюционном операторе для уравнения и = А(t)uрешение задачи Коши формально записывается в виде