|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АРКСИНУСА РАСПРЕДЕЛЕНИЕЗначение АРКСИНУСА РАСПРЕДЕЛЕНИЕ в математической энциклопедии: вероятностная мера на прямой, плотность к-рой равна нулю вне интервала (0, 1) п равна Наряду с А. р. используется обобщенное распределение арксинуса. Обобщенному А. р. соответствует функция распределения при Лит.:[1] Феллер В., Введение в теорию вероятностей н ее приложения, пер. с англ., т. 2, М., 1967; [2] Кендалл М. Дж., Стьюарт А., Теория распределений, пер. с англ., М., 1960. Б. <А. Рогозин. |
|
|
|
при 
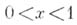Соответствующая функция распределения равна 
.
, к-рая имеет плотность 
, плотность 
совпадает с плотностью А. р. Обобщенное А. р. есть специальный случай бета-распределения. Момент 1-го порядка обобщенного А. р. равен 
, дисперсия этого же распределения равна 
. А. р. и обобщенное А. р. возникают при изучении флуктуации случайных блужданий, в теории восстановления (см. Арксинуса закон), а также используются в математич. статистике как специальные случаи бета -распределения.