|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО,Значение ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО, в математической энциклопедии:
цепь,- частично упорядоченное множество, в к-ром для любых двух элементов аи bимеет место что 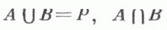 - пусто,  где  Классы Аи Вназ. нижним и верхним классами сечения. Различаются следующие типы сечений: скачок - в нижнем классе имеется наибольший элемент, а в верхнем - наименьший; д е д е к и н д о в о сечение - в нижнем (верхнем) классе имеется наибольший (наименьший) элемент, но в верхнем (нижнем) классе нет наименьшего (наибольшего); щель - в нижнем классе нет наибольшего элемента, а в верхнем - наименьшего. Л. у. м. наз. непрерывным, если все его сечения дедекиндовы. Подмножество DЛ. у. м. Рназ. плотным, если каждый не одноэлементный интервал множества Рсодержит элементы, принадлежащие D. Л. у. м. действительных чисел может быть охарактеризовано как непрерывное Л. у. м. в к-ром нет ни наибольшего, ни наименьшего элементов, но содержится счетное плотное подмножество. Всякое счетное Л. у. м. изоморфно некоторому подмножеству Л. у. м. всех двоичных дробей отрезка [0, 1]. Решетка Lизоморфна подмножеству Л. у. м. целых чисел тогда и только тогда, когда каждая ее подрешетка является ретрактом. Лит.:[1] Александров П. С., Введение в общую теорию множеств и функций, М.- Л., 1948; [2] его же, Введение в теорию множеств и общую топологию, М., 1977; [3] Бурбаки Н., Теория множеств, пер. с франц., М., 1965. Л. А. Скорняков. |
|
|
|
или 
Подмножество Л. у. м. само является Л. у. м. Всякий максимальный (минимальный) элемент Л. у. м. оказывается наибольшим (наименьшим). Важнейший частный случай Л. у. м. - вполне упорядоченные множества. Среди подмножеств частично упорядоченного множества, являющихся Л. у. м., особенно важную роль играет композиционный ряд. Сечением Л. <у. <м. Рназ. разбиение его на два подмножества Аи Втак,