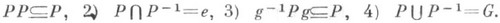" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЛИНЕЙНО УПОРЯДОЧЕННАЯ ГРУППА

Значение ЛИНЕЙНО УПОРЯДОЧЕННАЯ ГРУППА в математической энциклопедии:

алгебраическая система G, являющаяся группой относительно операции умножения, линейно упорядоченным множеством относительно бинарного отношения порядка и удовлетворяющая аксиоме: для любых элементов из следует

Множество положительных элементов Л. у. г. Gобладает свойствами: 1)

Обратно, если в группе G имеется множество P, удовлетворяющее свойствам 1) - 4), то Gможет быть превращена в Л. у. г., множество положительных элементов к-рой есть Р.

Имеется большое число признаков упорядочиваемости группы. Упорядочиваемые группы являются группами без кручения с однозначным извлечением корня. Упорядочиваемыми являются все абелевы группы без кручения, нильпотентные группы без кручения, свободные группы и свободные разрешимые группы. Существуют простые и нехопфовы Л. у. г. Факторгруппа упорядочиваемой группы по ее центру упорядочиваема.

Прямое, полное прямое и свободное произведения, а также сплетение Л. у. г. могут быть линейно упорядочены с продолжением порядков сомножителей. Группа, аппроксимируемая упорядочиваемыми группами, сама упорядочиваема. Для упорядочиваемых групп справедлива локальная теорема (см. Мальцева локальные теоремы). Л. у. г. вкладывается в мультипликативную группу линейно упорядоченного тела и в простую Л. у. г. Класс упорядочиваемых групп - аксиоматизируемый. Л. у. г. является топологической группой с интервальной топологией. Л. у. г. является архимедовой группой тогда и только тогда, когда она не имеет нетривиальных выпуклых подгрупп. Любая архимедова Л. у. г. изоморфна нек-рой подгруппе аддитивной группы действительных чисел с естественным порядком. Множество всех выпуклых подгрупп Л. у. г. образует полную инфраинвариантную систему, факторы к-рой архимедовы, и, значит, Л. у. г. обладают разрешимыми нормальными системами (см. Подгрупп система).

Специфическими для теории Л. у. г. являются вопросы, связанные с продолжением частичных порядков (см. Доупорядочиваемая группа). Имеется ряд обобщений понятия Л. у. г.

Лит.:[1] Кокорин А. И., Копытов В. М., Линейно упорядоченные группы, М., 1972; [2] Фукс Л., Частично упорядоченные алгебраические системы, пер. с англ., М., 1965; [3] Б у р б а к и Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965.

А. И. Кокорин, В. М. Копытов.