|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИЗначение ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФФИЦИЕНТАМИ в математической энциклопедии: - система дифференциальных уравнений  где  - почти периодические отображения; в координатной записи:  тде  есть система с интегральной разделенностью (см. Интегральной разделенности условие), то она почти периодическим по t Ляпунова преобразованием x=L(t)yприводится к диагональной системе y = B(t)yс почти периодич. коэффициентами, т. е. к такой, что существует не зависящий от tбазис в векторами оператора В(t);в координатах по этому базису система y=B(t)yзаписывается в диагональном виде:  Множество систем с интегральной разделенностью открыто в пространстве систем (2) с почти периодич. коэффициентами, наделенном метрикой 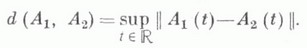 Имеет место следующая теорема. Пусть Для почти периодич. отображения Лит.:[1] Бор Г., Почти периодические функции, пер. с нем., М.- Л., 1934; [2] F a v а г 4 J., Lecons sur les fonctions prcsque periodiques, P., 1933; [3] Е р у г и н Н. П., Линейные системы обыкновенных дифференциальных уравнений с периодическими и квазипериодическими коэффициентами, Минск, 1963; [4] Массера X.-Л., Шеффер X.-X., Линейные дифференциальные уравнения и функциональные пространства, пер. с англ., М., 1970; [5] Мухамадиев Э., "Докл. АН СССР", 1971, т. 196, № 1, с. 47 - 49; [6] Итоги науки и техники. Математический анализ, т. 12, М., 1974, с. 71-146. В. М. Миллионщиков. |
|
|
|

 - почти периодич. числовые функции. Такие системы возникли в связи с появлением Бора почти периодических функций (см. [1]). Интерес к более узкому классу систем (A(t).и f(t) - квазипериодич. отображения) появился значительно раньше в связи с рассмотрением уравнений в вариациях вдоль условно периодич. решений уравнений небесной механики. Если однородная система
- почти периодич. числовые функции. Такие системы возникли в связи с появлением Бора почти периодических функций (см. [1]). Интерес к более узкому классу систем (A(t).и f(t) - квазипериодич. отображения) появился значительно раньше в связи с рассмотрением уравнений в вариациях вдоль условно периодич. решений уравнений небесной механики. Если однородная система  состоящий из векторов, являющихся при каждом
состоящий из векторов, являющихся при каждом  собственными
собственными  где
где  причем собственные значения Свсе действительны и различны,
причем собственные значения Свсе действительны и различны,  - почти периодич. отображение
- почти периодич. отображение  Тогда найдется
Тогда найдется  такое, что при всех e таких, что
такое, что при всех e таких, что  система (2) почти периодическим по tпреобразованием Ляпунова приводится к диагональной системе с почти периодич. коэффициентами.
система (2) почти периодическим по tпреобразованием Ляпунова приводится к диагональной системе с почти периодич. коэффициентами.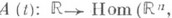
 следующие четыре утверждения эквивалентны друг другу: 1) для всякого почти периодич. отображения
следующие четыре утверждения эквивалентны друг другу: 1) для всякого почти периодич. отображения  у системы (1) найдется почти периодич. решение; 2) имеет место экспоненциальная дихотомия решений системы (2); 3) ни одна из систем
у системы (1) найдется почти периодич. решение; 2) имеет место экспоненциальная дихотомия решений системы (2); 3) ни одна из систем  где
где  не имеет ненулевых ограниченных решений; 4) для всякого ограниченного отображения
не имеет ненулевых ограниченных решений; 4) для всякого ограниченного отображения 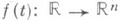 у системы (1) найдется ограниченное решение.
у системы (1) найдется ограниченное решение.