|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧАЗначение ЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА в математической энциклопедии: численные методы решения - методы, позволяющие получить решение Л. к. з. в виде таблицы его приближенных значений в точках сетки, не используя предварительной информации об ожидаемом виде решения. Для теории этих методов типично предположение о том, что решение исходной задачи существует и имеет достаточное число производных. Благодаря отсутствию других предположений численные методы отличаются своей универсальностью. Основой численных методов решения Л. к. з. является замена исходной системы уравнений ее сеточной аппроксимацией. В случае интегро-дифференциальных уравнений такая аппроксимация обычно строится с помощью разностных схем и квадратурных формул. При этом возникают следующие проблемы: 1) насколько быстро точное решение сеточной задачи сходится к решению исходной задачи при измельчении сетки; 2) насколько решение сеточной задачи чувствительно к изменениям исходных данных; 3) как найти, хотя бы приближенно, решение сеточной задачи. При решении первой и второй проблем используется следующий аппарат. Пусть в замкнутой области Dзадано уравнение  а на ее границе Г, состоящей из компонент Г i,- граничные условия  Здесь заданные непрерывные функции Пусть для аппроксимации уравнения (1) выбраны сетки Dh и  исходной задачи (1), (2). Пусть через  Если  то величина 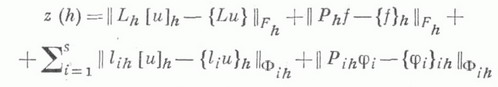 наз. погрешностью аппроксимации задачи (1), (2) задачей (3), (4). Если и - решение задачи (1), (2), то величина  наз. погрешностью аппроксимации на этом решении. Говорят, что задача (3), (4) аппроксимирует задачу (1), (2) (или аппроксимирует ее на решении и), если Пусть, напр., аппроксимируется уравнение теплопроводности. В квадранте  при начальном условии  а в качестве Ф 1 и Ф 2 - пространства непрерывных функций  соответственно. Пространство Uможно считать совпадающим с F, а в качестве Wберется подмножество функций  Оператор Lh может быть определен соотношением  и пусть  Для аппроксимации начального условия берется сетка Г 1h, состоящая из точек (0, mh), m=0, 1, 2, . . .; пространство Ф 1h сеточных функций  и  Для аппроксимации граничного условия берется сетка Г 2h, состоящая из точек  оператор 22h определяемый равенством  и оператор  Тогда  и  наз. корректной, если при достаточно малом hвыполняются следующие условия: эта задача разрешима при любых данных функциях  для любой функции 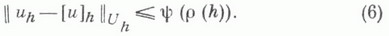 Если, кроме того, задача (3), (4) аппроксимирует задачу (1), (2) на решении и, то  при  справедливое для любой функции Для полного решения проблемы нахождения приближенного решения задачи (1), (2) необходимо построить точный или приближенный метод нахождения решения аппроксимации (3), (4), обладающий свойством устойчивости к округлениям. При исследовании устойчивости полезно использовать понятие замыкания вычислительного алгоритма. В приведенном примере уравнение целесообразно решать прогонки методом по переменной х. Оценка (6) погрешности сеточного метода обладает тем недостатком, что в выражение функции задачи (3), (4) с различными hи последующего выделения главной части погрешности вида  то  Иногда удается получить уравнения для функции z, содержащие производные от точного решения и. Тогда можно решать их численно на более грубой сетке после решения исходной задачи и по получении главной части погрешности добавить ее к приближенному решению uh и тем самым уточнить его. В некоторых случаях при специальном выборе координатных функций вариационного или проекционного метода решения задачи (1), (2) получаются уравнения вида (3), (4), обеспечивающие сходимость не только к классическому, но и к обобщенному решению. Этот способ построения аппроксимаций, наз. иногда методом конечных элементов, предоставляет большую свободу в выборе сетки. Возможность целесообразно располагать узлы позволяет достигать требуемой точности при меньшем числе узлов сетки. Лит.:[1] Бабушка И., В и т а с е к Э., Прагер М., Численные процессы решения дифференциальных уравнений, пер. с англ., М., 1969; [2] Бахвалов H. C., Конспекты по курсу "Основы вычислительной математики", ч. 4, М., 1968; [3] е г о ж е, Численные методы, 2 изд., М., 1975; [4] Варга Р., Функциональный анализ и теория аппроксимации в численном анализе, пер. с англ., М., 1974; [5] Гавурин М. К., Лекции по методам вычислений, М., 1971; [6] Годунов С. К., Рябенький В. С., Разностные схемы, 2 изд., М., 1977; [7] Д ь я к о н о в Е. Г., Разностные методы решения краевых задач, в. 1-2, М., 1971-72; [8] Канторович Л. В., А к и л о в Г. П., Функциональный анализ, 2 изд., М., 1977; [9] М а р ч у к Г. И., Методы вычислительной математики, 2 изд., М., 1980; [10] М и х л и н С. Г., Смолицкий X. Л., Приближенные методы решения дифференциальных и интегральных уравнений, М., 1965; [11] Р и х т м а й е р Р. Д., М о р т о н К., Разностные методы решения краевых задач, [пер. с англ.], М., 1972; [12] Рябенький В. С., Ф и л и п л о в А. Ф., Об устойчивости разностных уравнений, М., 1956; [13] Самарский А. А., Теория разностных схем, М., 1977; [14] Самарский А. А., Н и к о л а е в Е. С., Методы решения сеточных уравнений, М., 1978. А. Ф. Шапкин. |
|
|
|

 принадлежат нормированным линейным пространствам F, Ф i соответственно, а линейные операторы Lи li преобразуют нек-рое линейное подмножество Wнормированного линейного пространства Uфункций, непрерывных в D, в Fн Ф i соответственно.
принадлежат нормированным линейным пространствам F, Ф i соответственно, а линейные операторы Lи li преобразуют нек-рое линейное подмножество Wнормированного линейного пространства Uфункций, непрерывных в D, в Fн Ф i соответственно. зависящие от положительного параметра h;нормированные линейные пространства Uh и Fh функций и h и fh, определенных в точках сеток
зависящие от положительного параметра h;нормированные линейные пространства Uh и Fh функций и h и fh, определенных в точках сеток  соответственно, а также линейный оператор Lh, преобразующий Uh в Fh. Для аппроксимации граничного условия (2) выбирается сетка
соответственно, а также линейный оператор Lh, преобразующий Uh в Fh. Для аппроксимации граничного условия (2) выбирается сетка  нормированное линейное пространство Ф ih функций
нормированное линейное пространство Ф ih функций  определенных в точках сетки Г ih, и линейный оператор lih, преобразующий Uh, в Ф ih- Кроме того, выбираются линейные операторы Ph и pih, преобразующие Fи Ф i в Fh, и Ф ih соответственно. В результате получается сеточная аппроксимация
определенных в точках сетки Г ih, и линейный оператор lih, преобразующий Uh, в Ф ih- Кроме того, выбираются линейные операторы Ph и pih, преобразующие Fи Ф i в Fh, и Ф ih соответственно. В результате получается сеточная аппроксимация  обозначены следы функций
обозначены следы функций  из пространств U, F, Ф i на сетках
из пространств U, F, Ф i на сетках  соответственно. Исследование сходимости сеточных аппроксимаций и h к решению иисходной задачи при
соответственно. Исследование сходимости сеточных аппроксимаций и h к решению иисходной задачи при  имеет смысл производить лишь в сеточных нормах, согласованных с нормами в пространствах U, F, Ф i, т. е. при условии, что для любых функций
имеет смысл производить лишь в сеточных нормах, согласованных с нормами в пространствах U, F, Ф i, т. е. при условии, что для любых функций  выполняются предельные соотношения
выполняются предельные соотношения  (или
(или  ) при
) при  Порядок малости величины z(h).(или величины
Порядок малости величины z(h).(или величины  ) наз. порядком аппроксимации (или порядком аппроксимации на решении и).
) наз. порядком аппроксимации (или порядком аппроксимации на решении и). решается уравнение (1), где
решается уравнение (1), где  на полуоси
на полуоси 
 и граничном условии
и граничном условии  на полуоси
на полуоси  где
где  причем
причем 
 В качестве Fберется пространство непрерывных функций f (t, x).с нормой
В качестве Fберется пространство непрерывных функций f (t, x).с нормой  с нормами
с нормами 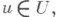 имеющих непрерывные частные производные
имеющих непрерывные частные производные  в области D. Пусть Df, - множество точек
в области D. Пусть Df, - множество точек  n=0, 1, 2, . . .; т=-1, 0, 1, . . ., где шаги сетки связаны функциональной зависимостью вида
n=0, 1, 2, . . .; т=-1, 0, 1, . . ., где шаги сетки связаны функциональной зависимостью вида  такой, что
такой, что  при
при  Множество
Множество  будет состоять из точек
будет состоять из точек  m=0, 1, 2, .... В качестве Fh и Uh выбираются пространства сеточных функций fh (t, x).и uh (t, x).с согласованными нормами
m=0, 1, 2, .... В качестве Fh и Uh выбираются пространства сеточных функций fh (t, x).и uh (t, x).с согласованными нормами  с согласованной нормой Х
с согласованной нормой Х  n = 0, 1, 2, ...; пространство Ф 2h сеточных функций
n = 0, 1, 2, ...; пространство Ф 2h сеточных функций  с согласованной нормой
с согласованной нормой  при
при  Если в качестве Wвзять более узкое множество функций
Если в качестве Wвзять более узкое множество функций  имеющих, кроме указанных ранее, ограниченные частные производные
имеющих, кроме указанных ранее, ограниченные частные производные  в области D, то при
в области D, то при  получают аппроксимацию второго порядка. Сеточную задачу
получают аппроксимацию второго порядка. Сеточную задачу  существует функция
существует функция  не зависящая от h, стремящаяся к нулю вместе с
не зависящая от h, стремящаяся к нулю вместе с  и такая, что
и такая, что  Решение корректной сеточной задачи равномерно по hнепрерывно зависит от данных функций. Корректность сеточной задачи является необходимым условием малой чувствительности ее решения к округлениям в процессе его вычисления. Если и - решение задачи (1), (2) и задача (3'), (4') корректна, то
Решение корректной сеточной задачи равномерно по hнепрерывно зависит от данных функций. Корректность сеточной задачи является необходимым условием малой чувствительности ее решения к округлениям в процессе его вычисления. Если и - решение задачи (1), (2) и задача (3'), (4') корректна, то  Если выполняются условия согласования норм, условие
Если выполняются условия согласования норм, условие  и условие (5), то, полагая uh=[u]h и переходя к пределу в неравенстве (5) при
и условие (5), то, полагая uh=[u]h и переходя к пределу в неравенстве (5) при  получают неравенство
получают неравенство  Таким образом, для исследования корректности краевых задач вида (1), (2) можно использовать такой путь: сначала получить оценку (5), а из нее оценку (7). С помощью оценок типа (5) часто удается доказать существование решения изадачи (1), (2) как предела сеточной аппроксимации и h при
Таким образом, для исследования корректности краевых задач вида (1), (2) можно использовать такой путь: сначала получить оценку (5), а из нее оценку (7). С помощью оценок типа (5) часто удается доказать существование решения изадачи (1), (2) как предела сеточной аппроксимации и h при 
 обычно входят производные от точного решения и. В нек-рых случаях удается априори (т. е. еще до решения задачи) оценить эти производные, однако такие оценки обычно оказываются грубыми. Несколько более точными являются оценки, в к-рых производные заменяются разностными отношениями приближенного решения и h. В основном же практич. оценка погрешности сеточных методов производится при помощи повторного решения
обычно входят производные от точного решения и. В нек-рых случаях удается априори (т. е. еще до решения задачи) оценить эти производные, однако такие оценки обычно оказываются грубыми. Несколько более точными являются оценки, в к-рых производные заменяются разностными отношениями приближенного решения и h. В основном же практич. оценка погрешности сеточных методов производится при помощи повторного решения  где g - известный порядок малости погрешности. Так, если справедливо асимптотич. соотношение
где g - известный порядок малости погрешности. Так, если справедливо асимптотич. соотношение