|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИНЕЙНАЯ ГРУППАЗначение ЛИНЕЙНАЯ ГРУППА в математической энциклопедии: - группа линейных преобразований векторного пространства Vконечной размерности n над нек-рым телом К. Выбор базиса в пространстве Vреализует Л. г. как группу невырожденных квадратных матриц степени пнад телом К. Тем самым устанавливается изоморфизм между линейными и матричными группами. Группа всех автоморфизмов свободного К-модуля Vназ. также полной линейной группе и и обозначается GL(F), а группа всех обратимых матриц порядка пнад К(также называемая полной Л. г.) обозначается GL(n, К)или GLn(K). Всякая подгруппа группы GL(V).наз. линейной группой степени п. Наиболее развитая часть теории Л. г. относится к случаю, когда тело Ккоммутативно, т. е. является полем. Поэтому в дальнейшем (если не оговорено противное) рассматриваются только Л. г. над полем. Теория Л. г. зародилась в середине 19 в. и развивалась в тесной связи с теорией групп Ли, теорией представлений групп и теорией Галуа. Начало систематич. исследованию Л. г. было положено работами К. Жордана (см. [1]). На первом этапе развития теории Л. г. в связи с потребностями теории Галуа изучались главным образом конечные Л. г., в особенности разрешимые и классические (см. Классическая группа). Было установлено и несколько общих фактов, связанных с приводимостью или неприводимостью Л. г. G, т. е. со свойствами G-модуля V. Для всякой Л. г. G существует композиционный ряд G-подмодулей  т. о. такой ряд, что все фактормодули Пусть G0 - подгруппа в G, состоящая из всех элементов, действующих тождественно на факторах Бесконечные линейные группы. Хотя теория Л. г. имеет довольно большую историю, общие методы в ней были созданы сравнительно недавно. Исключение составляют только разрешимые и классические Л. г. Еще К. Жордан в 1870 исследовал структуру разрешимых Л. г. над конечными полями и получил ряд классификационных результатов об этих группах. Эти исследования получили дальнейшее развитие (см. [13]): детально изучено строение и классифицированы максимальные разрешимые и локально нильпотентные подгруппы в GL ( п, К).над алгебраически замкнутым полем К. Основная структурная теорема о разрешимых Л. г. была получена А. И. Мальцевым (см. [8] с. 294- 313) в 1951: разрешимая Л. г. Г степени ге над алгебраически замкнутым полем обладает такой нормальной подгруппой Нконечного индекса, что Нсопряжена подгруппе треугольной группы, а индекс [Г : Н]меньше Важный и весьма разветвленный раздел теории Л. г. представляют классич. группы (см., напр., [4], [7]). Новый этап в развитии теории Л. г. начался в 60-е гг. 20 в., когда был создан общий метод исследования, базирующийся на технике алгебраич. групп (см. Линейная алгебраическая группа, а также [9], [18]). Этот метод позволил решить ряд проблем теории Л. г. Напр., с его помощью доказана теорема о свободных подгруппах Л. г. (см. [14]): всякая Л. г. над полем нулевой характеристики либо содержит неабелеву свободную подгруппу, либо обладает разрешимой подгруппой конечного индекса, и построена теория периодич. Л. г. (см. [9]) (оказалось, что основные структурные результаты теории конечных групп сохраняются и в более общем случае периодич. Л. г.). Другой важный метод теории Л. г., т. н. метод аппроксимации, был впервые применен А. И. Мальцевым в 1940 (см. [8] с. 58-73). Он годится для исследования Л. г. над областями целостности конечного типа, в частности для Л. г. с конечным числом образующих. Суть метода заключается в следующем: пусть GL(n, F)- полная Л. г. над конечно порожденным подкольцом Fполя К;тогда Fпо модулю максималвных идеалов аппроксимируется конечными полями Fi, что влечет аппроксимацию группы GL(n, F).конечными матричными группами GL(n, Fi). Для всякой подгруппы Конечные линейные группы. Наиболее крупным структурным результатом о конечных Л. г. до сих пор остается теорема Жордана (1878): существует такая целозначная функция f(n), что каждая конечная Л. г. степени пнад полем нулевой характеристики обладает абелевой нормальной подгруппой индекса меньше f(n). Для полей положительной характеристики существуют бесконечные серии простых конечных групп степени пи поэтому непосредственное перенесение теоремы Жордана на этот случай невозможно. Тем не менее с помощью техники модулярных представлений конечных групп доказано, что существует целозначная функция f((m, п).такая, что конечная Л. г. степени пнад полем характеристики р>0, порядок силовской р-подгруппы к-рой не превосходит р m, обладает абелевой нормальной подгруппой индекса меньше f((m, п).(см. [16]). Одной из главных проблем теории конечных Л. г. является проблема классификации простых конечных Л. г. С тех пор как в 1901 Л. Диксон изложил [2] основные факты о классич. простых конечных Л. г., было получено много новых результатов. Среди них центральное место занимают результаты К. Шевалле (см. [15]), применившего для исследования простых конечных Л. г. методы теории алгебраич. групп, что привело к открытию новых типов простых конечных Л. г. и позволило почти все известные простые конечные Л. г. получать единообразным методом (подробнее см. [11], [12]). Линейные группы над телами и кольцами. Систематич. исследование Л. г. над некоммутативным телом Кначалось после работы Ж. Дьёдонне (J. Dieudonne, 1943, см. [5]), в к-рой была описана конструкция определителя над телом (см. Определитель). Подгруппа группы GL(n, К).с определителем 1 наз. специальной линейной группой и обозначается SL(n, К). Она порождается трансвекциями (преобразованиями tтакими, что dim(l - t)V=1 и tv=v при Основные вопросы теории Л. г. над кольцами относятся к описанию нормальных подгрупп полной Л. г. и других классич. групп. Прогресс в этой области теснейшим образом связан с развитием алгебраич. К- теории (см. [5]). Так, задача описания нормальных подгрупп группы Изучались также автоморфизмы классических Л. г. над кольцами (см. [3], [19]). Лит.:[1] Jordan С., Traite des substitutions et des equations algebriques, P., 1870; [2] D i с k s о n L. E., Linear groups, Lpz., 1901; [3] Автоморфизмы классических групп, дер. с англ. и франц., М., 1976; [4] А р т и н Э., Геометрическая алгебра, пер. с англ., М., 1969; [5] Басс X., Алгебраическая K-теория, пер. с англ., М., 1973; [6] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [7] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974; [8] Мальцев А. И., Избранные труды, т. 1- Классическая алгебра, М., 1976, с. 58-73, 294 - 313; [9] Платонов В. П., "Изв. АН СССР. Сер. матем.", 1966, т. 30, № 3, с. 573-620; [10] его же, там же, 1976, т. 40, № 2, с. 227-61; [11] Семинар по алгебраическим группам, пер. с англ., М., 1973; [12] Стейнберг Р., Лекции о группах Шевалле, пер. с англ., М., 1975; [13] С у п р у н е н к о Д. А., Группы матриц, М., 1972; [14] Тите Ж., "Математика", 1972, т. 16, № 2, с. 47-66; [15] Шевалле К., там же, 1958, т. 2, М 1, с. 3-53; [16] Brauer R., Feit W., "Ann. Math.", 1966, v. 84, №1, p. 119-31; [17] Draxl P., Kneser M., SKi von Schiefkorpern, В.- Hdlb.-N. Y., 1980; [18] Wehrfritz В., Infinite linear groups, В.- Hdlb.- N. Y., 1973; [191 Итоги науки. Алгебра. Топология. Геометрия, 1970, М., 1971, с. 75-110. В. П. Платонов. |
|
|
|

 неприводимы. Другими словами, всякая матричная группа сопряжена в GLn(K). нек-рой группе квазитреугольного вида с неприводимыми диагональными блоками.
неприводимы. Другими словами, всякая матричная группа сопряжена в GLn(K). нек-рой группе квазитреугольного вида с неприводимыми диагональными блоками.  Тогда G0- нормальная нильпотентная подгруппа, элементы к-рой удовлетворяют (в K-алгебре End(V) всех линейных преобразований пространства V).уравнению
Тогда G0- нормальная нильпотентная подгруппа, элементы к-рой удовлетворяют (в K-алгебре End(V) всех линейных преобразований пространства V).уравнению 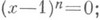 такие Л. г. наз. унипотентными. Всякая унипо-тентная группа, рассматриваемая как матричная группа, сопряжена в GL ( п, К).с нек-рой подгруппой группы верхних треугольных матриц с единичной диагональю. В существенной мере строение группы Gпо модулю G0 определяется строением неприводимых Л. г. Gi+1, индуцируемых Gв факторах Vi+1/Vi. Если Л. г. Gнеприводима над алгебраически замкнутым полем К, то Gсодержит п 2 линейно независимых над Кэлементов K-алгебры End(V), т. е. K-линейная оболочка Gсовпадает с End(V). Всякая нормальная подгруппа вполне приводимой Л. г. вполне приводима.
такие Л. г. наз. унипотентными. Всякая унипо-тентная группа, рассматриваемая как матричная группа, сопряжена в GL ( п, К).с нек-рой подгруппой группы верхних треугольных матриц с единичной диагональю. В существенной мере строение группы Gпо модулю G0 определяется строением неприводимых Л. г. Gi+1, индуцируемых Gв факторах Vi+1/Vi. Если Л. г. Gнеприводима над алгебраически замкнутым полем К, то Gсодержит п 2 линейно независимых над Кэлементов K-алгебры End(V), т. е. K-линейная оболочка Gсовпадает с End(V). Всякая нормальная подгруппа вполне приводимой Л. г. вполне приводима. где
где  - нек-рая эффективно определяемая функция от п;в частности, коммутант группы Нявляется унипотентной группой и, с абстрактной точки зрения, группа Г есть конечное расширение группы Нс нильпотентным коммутантом.
- нек-рая эффективно определяемая функция от п;в частности, коммутант группы Нявляется унипотентной группой и, с абстрактной точки зрения, группа Г есть конечное расширение группы Нс нильпотентным коммутантом. получается индуцируемая аппроксимация конечными Л. г. Г i. Оказывается, во многих случаях свойства группы Г в сильной степени определяются свойствами групп Г i. Этот метод был позднее усовершенствован (см. [18]), что привело к доказательству общей аппроксимационной теоремы, из к-рой выводится большинство результатов о бесконечных Л. г. с конечным числом образующих.
получается индуцируемая аппроксимация конечными Л. г. Г i. Оказывается, во многих случаях свойства группы Г в сильной степени определяются свойствами групп Г i. Этот метод был позднее усовершенствован (см. [18]), что привело к доказательству общей аппроксимационной теоремы, из к-рой выводится большинство результатов о бесконечных Л. г. с конечным числом образующих. и всякая подгруппа группы GL(n, К), инвариантная относительно GL(n, К), либо скалярна, либо содержит SL(n, K), за исключением случаен n=2, | К| =2,3, когда группа GL(2, К).разрешима. Если тело Кконечномерно над своим центром Z, то существует единственный определитель со значениями в Z, называемый приведенной нормой (см. [5]), причем SL(n, К).содержится в группе UL(n, К).элементов с приведенной нормой 1. Вопрос о совпадении этих групп, поставленный в 1943 (проблема Т а н а к и - А р т и н а), был решен отрицательно в [10]. Группа UL(n, К).и факторгруппа
и всякая подгруппа группы GL(n, К), инвариантная относительно GL(n, К), либо скалярна, либо содержит SL(n, K), за исключением случаен n=2, | К| =2,3, когда группа GL(2, К).разрешима. Если тело Кконечномерно над своим центром Z, то существует единственный определитель со значениями в Z, называемый приведенной нормой (см. [5]), причем SL(n, К).содержится в группе UL(n, К).элементов с приведенной нормой 1. Вопрос о совпадении этих групп, поставленный в 1943 (проблема Т а н а к и - А р т и н а), был решен отрицательно в [10]. Группа UL(n, К).и факторгруппа 
 называемая приведенной группой У а и т х е д а, играют важную роль в теории линейных алгебраич. групп и алгебраич. K-теории [5].
называемая приведенной группой У а и т х е д а, играют важную роль в теории линейных алгебраич. групп и алгебраич. K-теории [5].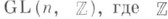 - кольцо целых чисел, фактически эквивалентна конгруэнц-проблеме для группы
- кольцо целых чисел, фактически эквивалентна конгруэнц-проблеме для группы  при n>2. А именно, всякая нескалярная нормальная подгруппа группы
при n>2. А именно, всякая нескалярная нормальная подгруппа группы  n>2, имеет конечный индекс и является конгруэнц-подгруппой, в то время как группа
n>2, имеет конечный индекс и является конгруэнц-подгруппой, в то время как группа  есть конечное расширение свободной группы и потому обладает разнообразными нормальными подгруппами бесконечного индекса.
есть конечное расширение свободной группы и потому обладает разнообразными нормальными подгруппами бесконечного индекса.