"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИ РЕДУКТИВНАЯ АЛГЕБРАЗначение ЛИ РЕДУКТИВНАЯ АЛГЕБРА в математической энциклопедии:
- конечномерная алгебра Ли над полем kхарактеристики 0, присоединенное представление к-рой вполне приводимо. Свойство редуктивности алгебры Ли  равносильно любому из следующих свойств: равносильно любому из следующих свойств:
1) 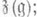 радикал радикал 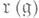 алгебры Ли алгебры Ли 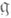 совпадает с центром совпадает с центром
2)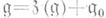 , где , где  - полупростой идеал в - полупростой идеал в  ; ;
3) где где 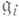 - простые идеалы; - простые идеалы;
4)  допускает точное вполне приводимое конечномерное линейное представление. допускает точное вполне приводимое конечномерное линейное представление.
Свойство редуктивности алгеб, ры Ли сохраняется как при расширении, так и при сужении основного поля k.
Важный класс Ли р. а. над  составляют компактные алгебры Ли (см. Ли компактная группа). Группу Ли, алгебра Ли к-рой редуктивна, часто наз. р е д у к т и в н о й группой Ли. Если kалгебраически замкнуто, то алгебра Ли над kявляется редуктивной тогда и только тогда, когда она изоморфна алгебре Ли нек-рой редуктивной алгебраич. группы над k. составляют компактные алгебры Ли (см. Ли компактная группа). Группу Ли, алгебра Ли к-рой редуктивна, часто наз. р е д у к т и в н о й группой Ли. Если kалгебраически замкнуто, то алгебра Ли над kявляется редуктивной тогда и только тогда, когда она изоморфна алгебре Ли нек-рой редуктивной алгебраич. группы над k.
Обобщением понятия Ли р. а. является следующее понятие. Подалгебра  конечномерной алгебры Ли конечномерной алгебры Ли  над kназ. редуктивной в над kназ. редуктивной в  если присоединенное представление ad: если присоединенное представление ad: 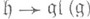 вполне приводимо. В этом случае вполне приводимо. В этом случае  будет Ли р. а. Если kалгебраически замкнуто, то для редуктивности подалгебры будет Ли р. а. Если kалгебраически замкнуто, то для редуктивности подалгебры  в в  необходимо и достаточно следующее условие: необходимо и достаточно следующее условие:  состоит из полупростых линейных преобразований. состоит из полупростых линейных преобразований.
Лит.:[1] С е р р Ж.- П., Алгебры Ли и группы Ли, пер. с англ, и франц., М., 1969. А. Л. Онищик.
|

 равносильно любому из следующих свойств:
равносильно любому из следующих свойств: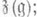 радикал
радикал 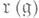 алгебры Ли
алгебры Ли 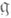 совпадает с центром
совпадает с центром 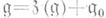 , где
, где  - полупростой идеал в
- полупростой идеал в  ;
; где
где 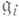 - простые идеалы;
- простые идеалы; допускает точное вполне приводимое конечномерное линейное представление.
допускает точное вполне приводимое конечномерное линейное представление. составляют компактные алгебры Ли (см. Ли компактная группа). Группу Ли, алгебра Ли к-рой редуктивна, часто наз. р е д у к т и в н о й группой Ли. Если kалгебраически замкнуто, то алгебра Ли над kявляется редуктивной тогда и только тогда, когда она изоморфна алгебре Ли нек-рой редуктивной алгебраич. группы над k.
составляют компактные алгебры Ли (см. Ли компактная группа). Группу Ли, алгебра Ли к-рой редуктивна, часто наз. р е д у к т и в н о й группой Ли. Если kалгебраически замкнуто, то алгебра Ли над kявляется редуктивной тогда и только тогда, когда она изоморфна алгебре Ли нек-рой редуктивной алгебраич. группы над k. конечномерной алгебры Ли
конечномерной алгебры Ли  над kназ. редуктивной в
над kназ. редуктивной в  если присоединенное представление ad:
если присоединенное представление ad: 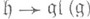 вполне приводимо. В этом случае
вполне приводимо. В этом случае  будет Ли р. а. Если kалгебраически замкнуто, то для редуктивности подалгебры
будет Ли р. а. Если kалгебраически замкнуто, то для редуктивности подалгебры  в
в  необходимо и достаточно следующее условие:
необходимо и достаточно следующее условие:  состоит из полупростых линейных преобразований.
состоит из полупростых линейных преобразований.