"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АРИФМЕТИЧЕСКИЙ РЯД
Значение АРИФМЕТИЧЕСКИЙ РЯД в математической энциклопедии:
порядка т- последовательность значений многочлена степени т:
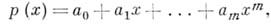
принимаемых им при последовательных целых, неотрицательных значениях переменной 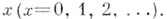 Если
Если 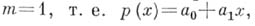 получается арифметич. прогрессия с начальным членом
получается арифметич. прогрессия с начальным членом  и разностью
и разностью 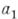 . При
. При  или
или 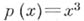 получаются последовательности квадратов или кубов целых чисел - частные случаи А. р. 2-го и 3-го порядков. Если составить ряд из разностей соседних членов А. р., затем для полученной последовательности разностей также образовать их разности (вторые разности), для вторых разностей образовать разности (третьи разности) и т. д., то на m-м этапе окажется, что все (m-ые) разности равны между собой. Обратно, если для нек-рой последовательности чисел ее m-ые разности равны между собой, то эта последовательность есть А. р. порядка т.
получаются последовательности квадратов или кубов целых чисел - частные случаи А. р. 2-го и 3-го порядков. Если составить ряд из разностей соседних членов А. р., затем для полученной последовательности разностей также образовать их разности (вторые разности), для вторых разностей образовать разности (третьи разности) и т. д., то на m-м этапе окажется, что все (m-ые) разности равны между собой. Обратно, если для нек-рой последовательности чисел ее m-ые разности равны между собой, то эта последовательность есть А. р. порядка т.
Пользуясь этим свойством, можно строить А. р. различных порядков, отправляясь от их разностей. Напр., последовательность единиц: 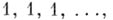 можно рассматривать как первые разности последовательности натуральных чисел:
можно рассматривать как первые разности последовательности натуральных чисел: 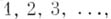 - как вторые разности последовательности треугольных чисел:
- как вторые разности последовательности треугольных чисел: 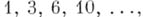 - как третьи разности последовательности тетраэдр и ческих чисел:
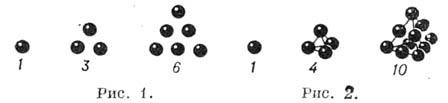
- как третьи разности последовательности тетраэдр и ческих чисел: 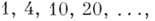 и т. д. Названия этих чисел объясняются тем, что треугольные числа выражают числа шаров, уложенных в виде треугольника (рис. 1), а тетра-эдрические - в виде тетраэдра (пирамиды) (рис. 2). Треугольные числа выражаются формулой
и т. д. Названия этих чисел объясняются тем, что треугольные числа выражают числа шаров, уложенных в виде треугольника (рис. 1), а тетра-эдрические - в виде тетраэдра (пирамиды) (рис. 2). Треугольные числа выражаются формулой 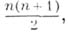 а тетраэдрические - формулой
а тетраэдрические - формулой
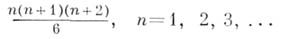
Обобщением треугольных чисел являются k-yгольные, или фигурные числа, игравшие важную роль на разных этапах развития арифметики, k-угольные числа имеют вид:
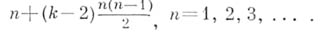
Они образуют А. р. 2-го порядка, с первым членом 1, вторым членом 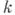 и вторыми разностями
и вторыми разностями 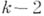 . При
. При 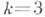 получаются треугольные числа, при
получаются треугольные числа, при 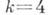 - квадратные
- квадратные 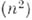 , при
, при 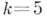 - пентагональные (пятиугольные)
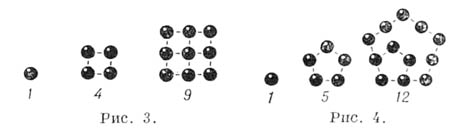
- пентагональные (пятиугольные) 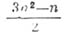 и т. п. Названия эти поясняются на рис. 3 и 4, где числа шаров, расположенных в виде квадрата или пятиугольника, выражаются соответствующими квадратными или пеитагональными числами. Относительно фигурных чисел справедлива следующая теорема, высказанная П. Ферма (P. Fermat) и доказанная впервые О. Коши (A. Cauchy): любое натуральное число можно представить в виде суммы не более, чем kfc-угольных чисел.
и т. п. Названия эти поясняются на рис. 3 и 4, где числа шаров, расположенных в виде квадрата или пятиугольника, выражаются соответствующими квадратными или пеитагональными числами. Относительно фигурных чисел справедлива следующая теорема, высказанная П. Ферма (P. Fermat) и доказанная впервые О. Коши (A. Cauchy): любое натуральное число можно представить в виде суммы не более, чем kfc-угольных чисел.
Лит.:[1] Ван-дер-Варден Б. Л., Современная алгебра, пер. с нем., 2 изд., ч. 1, М.-Л., 1947; Г2] Арнольд И. В., Теоретическая арифметика, 2 изд., М., 1939. БСЭ-2.

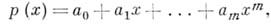
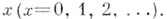 Если
Если 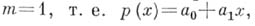 получается арифметич. прогрессия с начальным членом
получается арифметич. прогрессия с начальным членом  и разностью
и разностью 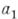 . При
. При  или
или 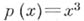 получаются последовательности квадратов или кубов целых чисел - частные случаи А. р. 2-го и 3-го порядков. Если составить ряд из разностей соседних членов А. р., затем для полученной последовательности разностей также образовать их разности (вторые разности), для вторых разностей образовать разности (третьи разности) и т. д., то на m-м этапе окажется, что все (m-ые) разности равны между собой. Обратно, если для нек-рой последовательности чисел ее m-ые разности равны между собой, то эта последовательность есть А. р. порядка т.
получаются последовательности квадратов или кубов целых чисел - частные случаи А. р. 2-го и 3-го порядков. Если составить ряд из разностей соседних членов А. р., затем для полученной последовательности разностей также образовать их разности (вторые разности), для вторых разностей образовать разности (третьи разности) и т. д., то на m-м этапе окажется, что все (m-ые) разности равны между собой. Обратно, если для нек-рой последовательности чисел ее m-ые разности равны между собой, то эта последовательность есть А. р. порядка т. 

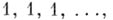 можно рассматривать как первые разности последовательности натуральных чисел:
можно рассматривать как первые разности последовательности натуральных чисел: 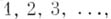 - как вторые разности последовательности треугольных чисел:
- как вторые разности последовательности треугольных чисел: 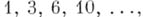 - как третьи разности последовательности тетраэдр и ческих чисел:
- как третьи разности последовательности тетраэдр и ческих чисел: 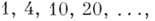 и т. д. Названия этих чисел объясняются тем, что треугольные числа выражают числа шаров, уложенных в виде треугольника (рис. 1), а тетра-эдрические - в виде тетраэдра (пирамиды) (рис. 2). Треугольные числа выражаются формулой
и т. д. Названия этих чисел объясняются тем, что треугольные числа выражают числа шаров, уложенных в виде треугольника (рис. 1), а тетра-эдрические - в виде тетраэдра (пирамиды) (рис. 2). Треугольные числа выражаются формулой 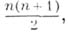 а тетраэдрические - формулой
а тетраэдрические - формулой 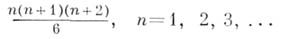
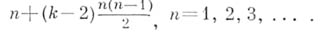
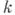 и вторыми разностями
и вторыми разностями 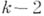 . При
. При 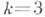 получаются треугольные числа, при
получаются треугольные числа, при 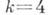 - квадратные
- квадратные 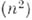 , при
, при 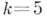 - пентагональные (пятиугольные)
- пентагональные (пятиугольные) 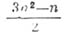 и т. п. Названия эти поясняются на рис. 3 и 4, где числа шаров, расположенных в виде квадрата или пятиугольника, выражаются соответствующими квадратными или пеитагональными числами. Относительно фигурных чисел справедлива следующая теорема, высказанная П. Ферма (P. Fermat) и доказанная впервые О. Коши (A. Cauchy): любое натуральное число можно представить в виде суммы не более, чем kfc-угольных чисел.
и т. п. Названия эти поясняются на рис. 3 и 4, где числа шаров, расположенных в виде квадрата или пятиугольника, выражаются соответствующими квадратными или пеитагональными числами. Относительно фигурных чисел справедлива следующая теорема, высказанная П. Ферма (P. Fermat) и доказанная впервые О. Коши (A. Cauchy): любое натуральное число можно представить в виде суммы не более, чем kfc-угольных чисел.