"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРАЗначение ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРА в математической энциклопедии:
- 1) Алгебра Ли алгебраич. подгруппы (см. Алгебраическая группа).полной линейной группы, всех автоморфизмов конечномерного векторного пространства Vнад полем k. Если 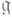 - произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая - произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая  она наз. алгебраической оболочкой подалгебры Ли она наз. алгебраической оболочкой подалгебры Ли  Для алгебраичности алгебры Лн Для алгебраичности алгебры Лн  над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором  в в  лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы 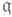 была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли  состоит в том, что вместе с га и состоит в том, что вместе с га и 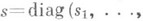  в в  лежат все операторы вида лежат все операторы вида 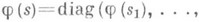  где где  - произвольное - произвольное  -линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0. -линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.
2) Алгебра Ли Lнад коммутативным кольцом k, в к-рой для любого элемента 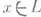 -эндоморфизм -эндоморфизм 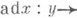  заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр. заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.
Лит.:[1] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Ш е в а л л е К., Теория групп Ли, пер. с франц., т. 2, М., 1958; [3] S е 1 i g m a n G., Modular Lie algebras, В.- Hdlb.- N. Y., 1967; [4] Голод Е. С., "Изв. АН СССР. Сер. матем.", 1964, т. 28, № 2, с. 273-76.
Ю. А. Бахтурин.
|

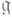 - произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая
- произвольная подалгебра в алгебре Ли всех эндоморфизмов V, то существует наименьшая Ли а. а., содержащая  она наз. алгебраической оболочкой подалгебры Ли
она наз. алгебраической оболочкой подалгебры Ли  Для алгебраичности алгебры Лн
Для алгебраичности алгебры Лн  над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором
над произвольным алгебраически замкнутым полем kнеобходимо, чтобы вместе с каждым линейным оператором  в
в  лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы
лежали его полупростая и нильпотентная компоненты sи п(см. Жордана разложение). Это условие определяет т. н. почти алгебраические алгебры Ли. Оно не является достаточным для того, чтобы 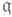 была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли
была Ли а. а. В случае поля kхарактеристики 0 необходимое и достаточное условие алгебраичности алгебры Ли  состоит в том, что вместе с га и
состоит в том, что вместе с га и 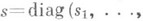
 в
в  лежат все операторы вида
лежат все операторы вида 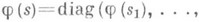
 где
где  - произвольное
- произвольное 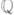 -линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.
-линейное отображение из kв k. Исследовано [3] строение Ли а. а. в случае поля характеристики р> 0.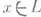 -эндоморфизм
-эндоморфизм 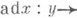
 заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.
заданный на L, является корнем нек-рого многочлена со старшим коэффициентом 1 и остальными коэффициентами из k. Конечномерная над полем kалгебра Ли является Ли а. а. Обратное неверно: над любым полем kсуществуют бесконечномерные Ли а. а. с конечным числом порождающих [4]. Ряд вопросов о Ли а. а. получает решение уже в классе Ли нильалгебр.