" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЛЕФШЕЦА ТЕОРЕМА

Значение ЛЕФШЕЦА ТЕОРЕМА в математической энциклопедии:

- 1) Л. т. о неподвижных точках, Лефшеца - Хопфа теорема,- теорема, позволяющая выразить число неподвижных точек непрерывного отображения через его Лефшеца число. Так, если непрерывное отображение f: конечного клеточного пространства Xне имеет неподвижных точек, то его число Лефшеца L(f) равно нулю. Частным случаем последнего утверждения является Брауэра теорема о неподвижной точке.

Ю. Б. Рудяк.

2) Л. т. о г и п е р п л о с к о м сечении, слабая Л. т.: пусть X - алгебраич. подмногообразие комплексной размерности пв комплексном проективном пространстве и пусть - гиперплоскость, проходящая через все особые точки многообразия X(если они есть), а - гиперплоское сечение многообразия X;тогда относительные группы гомологии равны нулю при i<n. Отсюда вытекает, что естественный гомоморфизм

является изоморфизмом для i<n-1 и сюръективен для i=n-1 (см. [1]).

По формулам универсальных коэффициентов отсюда получаются соответствующие утверждения для групп целочисленных когомологии. Во всяком случае для когомологий с коэффициентами в поле рациональных чисел имеют место двойственные утверждения: гомоморфизм пространств когомологии индуцированный вложением является изоморфизмом для i<n-1 и инъективен для i=n-1 (см. [6]). Аналогичное утверждение справедливо для гомото-пич. групп: при i<n. В частности, кано-нич. гомоморфизм (X).является изоморфизмом при и сюръективен при n=2 (теорема Лефшеца о фундаментальной группе). Существует обобщение этой теоремы на случай произвольного алгебраически замкнутого поля (см. [7]), а также на случай, когда У - нормальное полное пересечение в X(см. [8]).

3) Сильная Л. т.- теорема о существовании разложения Лефшеца когомологий комплексного кэлерова многообразия на примитивные составляющие.

Пусть V - компактное кэлерово многообразие размерности пс кэлеровой формой о) и пусть

- класс когомологий типа (1, 1), соответствующий форме со при изоморфизме де Рама (если V - проективное алгебраич. многообразие над с естественной метрикой Ходжа, то -класс когомологий, двойственный классу гомологии гиперплоского сечения) и

- линейный оператор, определяемый умножением на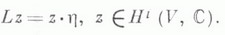

т. <е.

Имеет место изоморфизм (см. [1])

для любого k=0, 1,. . ., п. Ядро оператора

обозначается и наз. примитивной частью (n-k)-когомологий многообразия V. Элементы из наз. прилитивными когомологиями, а соответствующие им циклы - примитивными циклами. Сильная Л. т. устанавливает следующее разложение когомологий в прямую сумму примитивных (наз. разложением Лефшеца):

для всех m=0, 1, 2, . . ., 2n. Отображения

являются вложениями. Разложение Лефшеца коммутирует с разложением Ходжа

(см. [13]). В частности, определена примитивная часть

и

Сильная Л. т. и разложение Лефшеца имеют аналоги в абстрактной алгебраич. геометрии для l-адических и кристальных когомологий (см. [4], [14]).

4) Л. т. о к о г о м о л о г и я х типа (1,1) - теорема о соответствии между двумерными алгебраич. классами когомологий комплексного проективного алгебраич. многообразия и классами когомологий типа (1, 1).

Пусть V - неособое проективное алгебраич. многообразие над полем Элемент наз. а л г е б р а и ч е с к и м, если двойственный ему (в смысле Пуанкаре) класс гомологии определяется нек-рым дивизором. Л. т. о когомологиях типа (1,1) утверждает, что класс алгебраичен тогда и только тогда, когда

где - компонента Ходжа типа (1, 1) двумерных комплексных когомологий а отображение индуцировано естественным вложением (см. [1], а также [6], [12]).

По поводу алгебраич. классов когомологий в размерностях, больших 2, см. Ходжа гипотеза.

Для произвольного комплексного аналитич. многообразия Vсуществует аналогичная характеризация элементов группы являющихся классами Чжэня расслоений на комплексные прямые над V(см. [11]).

Лит.:[1] Lefschetz S., L'analysis situs et la geometrie algebrique, P., 1924; [2] его же, "Trans. Amer. Math. Soc.", 1921, v. 22, p. 327-482; [3] его же, "Ann. Math.", 1937, v. 38, p. 819-22; [4] Berthelot P., Cohomologie cristalllne des schemas de caracteristique r>0,B.- [a. o.], 1974; [5] De1igne P., Katz N., Groupes de monodromie en geometric algebrique, В.- [a. o.], 1973; [6] Griffiths P., Harris J., Principles of algebraic geometry, N. Y., 1978; [7] G r о t h e n d i e с k A., Cohomologie locale des faisceaux coherents et theoremes de Lefschetz locaux et globaux, P.- Amst., 1968; [8] Наrtshorne R., Ample subvarieties of algebraic varieties, B.- [u. a.], 1970; [9] М а м ф о р д Д., Абелевы многообразия, пер. с англ., М., 1971; [101 Милнор Д ш., Теория Морса, пер. с англ., М., 1965; [11] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [12] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [13] Вейль А., Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961; [14] Д е л и н ь П., "Успехи матсм. наук", 1975, т. 30, в. 5, с. 159-90.

В. А. Псковских.