|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АРИФМЕТИЧЕСКАЯ ФУНКЦИЯЗначение АРИФМЕТИЧЕСКАЯ ФУНКЦИЯ в математической энциклопедии: теоретико-числовая функция,- комплекснозначная функция, областью определения к-рой может служить одно из множеств: множество натуральных чисел, множество целых рациональных чисел, множество целых идеалов фиксированного алгебранч. числового поля, решетка в многомерном координатном пространстве и т. п. Это - А. ф. в широком смысле. Однако часто под А. ф. понимается функция указанного типа, обладающая нек-рымн специальными арифметич. свойствами. Наиболее употребительные А. ф. имеют традиционные символич. обозначения: Напр., в алгебраич. поле Кстепени пдля целого идеала А. ф. возникают и используются при изучении свойств чисел. Однако теория А. ф. представляет и самостоятельный интерес. Закономерность изменения А. <ф. обычно не удается охарактеризовать простыми формулами - ищется асимптотика числовых функций. Так как многие А. ф. не монотонны, то большое значение имеет изучение средних значений функций. Важный класс А. ф. составляют мультипликативные арифметические функции и аддитивные арифметические функции. В вероятностной теории чисел изучается вопрос о распределении их значений [5]. Лит.:[1] Виноградов И. М.,Основы теории чисел, 8 изд., М., 1972; [2] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [3] Xуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. е .нем., М., 1964; [4] Чандрасек харан К., Арифметические функции, пер. с англ., М., 1975; [5] Кубилю с И., Вероятностные методы в теории чисел, 2 изд., Вильнюс, 1962. Н. И. Климов.
|
|
|
|

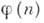 - Эйлера функция,
- Эйлера функция,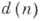 или
или 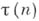 - делителей число,
- делителей число,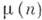 - Мёбиуса функция,
- Мёбиуса функция, 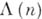 - Манголъдта функция,
- Манголъдта функция, 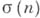 - сумма делителей числа п. К А. ф. относят также целую часть числа
- сумма делителей числа п. К А. ф. относят также целую часть числа 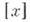 и дробную часть числа
и дробную часть числа 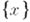 . Изучаются А. ф., выражающие число решений уравнения; напр.,
. Изучаются А. ф., выражающие число решений уравнения; напр., 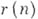 - число решений в целых числах
- число решений в целых числах 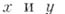 . уравнения
. уравнения 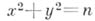 в Гольдбаха проблеме:
в Гольдбаха проблеме: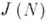 - число решений в простых числах уравнения
- число решений в простых числах уравнения 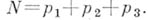 Другие А. ф. выражают количество чисел с к.-л. условиями; напр., функция
Другие А. ф. выражают количество чисел с к.-л. условиями; напр., функция 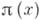 - число простых чисел, не превосходящих х, характеризует распределение простых чисел;
- число простых чисел, не превосходящих х, характеризует распределение простых чисел; 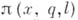 - число не превосходящих хпростых чисел в арифметич. прогрессии
- число не превосходящих хпростых чисел в арифметич. прогрессии 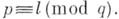 Со свойствами простых чисел связаны также Чебышева функции:
Со свойствами простых чисел связаны также Чебышева функции: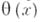 - сумма натуральных логарифмов простых чисел до
- сумма натуральных логарифмов простых чисел до 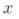 и
и 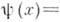
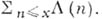 В алгебраич. теории чисел рассматриваются обобщения названных А. ф. натурального аргумента.
В алгебраич. теории чисел рассматриваются обобщения названных А. ф. натурального аргумента.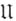 вводится функция Эйлера
вводится функция Эйлера 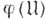 - число классов вычетов по идеалу
- число классов вычетов по идеалу 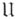 , взаимно простых с
, взаимно простых с