|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛЕВИ - КРАМЕРА ТЕОРЕМАЗначение ЛЕВИ - КРАМЕРА ТЕОРЕМА в математической энциклопедии: если сумма двух независимых непостоянных случайных величин нормально распределена, то и каждое из слагаемых нормально распределено; высказана П. Леви [1] и доказана Г. Крамером [2]. Эквивалентные формулировки: 1) если композиция двух собственных распределений является нормальным распределением, то и каждое из них является нормальным распределением; 2) если 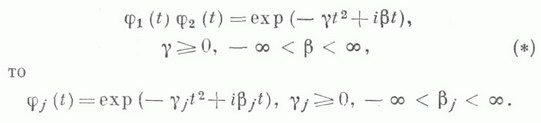 В формулировке 1) Л.- К. т. допускает обобщение на композицию двух знакопеременных мер с ограничениями на отрицательную вариацию; в формулировке 2) - на случай, когда вместо условия (*) рассматривается условие 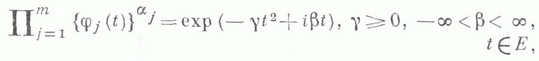 где Л.-К. т. обладает свойством устойчивости, т. е. близость распределения суммы независимых случайных величин к нормальному влечет близость распределения каждого из слагаемых к нормальному; известны количественные оценки устойчивости. Теоремы, аналогичные Л. - К. т., получены для распределения Пуассона, для композиции распределения Пуассона и нормального, для других классов безгранично делимых распределений (см. [6]). Лит.:[1] Lev у P., "J. math, pures et appl.", 1935, t. 14, p. 347 - 402; [2] С r a m e rH., "Math. Z.", 1936, Bd 41, S. 405- 14; [3] Райков Д. А., "Докл. АН СССР", 1937, т. 14, с. 9-12; [4] Л и н н и к Ю. В., "Теория вероятн. и ее примен.", 1957, т. 2, с. 34-59; [5] С а п о г о в Н. А., "Вести. Ленингр. ун-та. Сер. матем., механ. и астр.", 1959, М" 19, с. 78-105; [6] Л и н н и к Ю. В., О с т р о в с к и й И. В., Разложения случайных величин и векторов, М., 1972; [7] Ф е л ь д м а н Г. М., "Теория вероятн. и ее примен.", 1977, т. 22, вып. 1, с. 136-43. И. В. Островский. |
|
|
|

 - характеристич. функции и
- характеристич. функции и  - характеристич. функции,
- характеристич. функции, 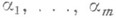 - положительные числа, Е - множество действительных чисел с точкой сгущения в нуле. Имеются обобщения Л. - К. т. на случайные величины в евклидовых пространствах и в локально компактных абелевых группах.
- положительные числа, Е - множество действительных чисел с точкой сгущения в нуле. Имеются обобщения Л. - К. т. на случайные величины в евклидовых пространствах и в локально компактных абелевых группах.