|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛЕВИ МЕТРИКАЗначение ЛЕВИ МЕТРИКА в математической энциклопедии: - метрика Lв пространстве  для любых F, Важнейшие свойства Л. <м.: 1) Л. м. индуцирует в  то для любых 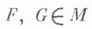  3) Регулярность Л. м.: для любых   следствием этого свойства является свойство полуаддитивности :  и "неравенство сглаживания":  (Е- распределение, вырожденное в нуле). 4) Если  то  5) Если  - абсолютный момент распределения F, то  6) Л. м. на Мсвязана со средней метрикой 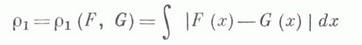 неравенством  7) Л. м. на Мсвязана с равномерной метрикой  соотношениями 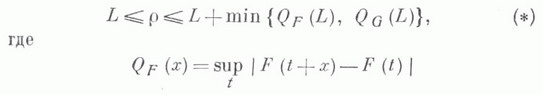 (QF(x) - концентрации функция, если  Следствием (*) является теорема Пойа - Гливенко об эквивалентности слабой и равномерной сходимости в том случае, когда предельное распределение непрерывно. 8) Если  - константы, то для любых   (в частности, Л. м. инвариантна относительно сдвига распределений) и  9) Если f, g - характеристич. функции, соответствующие распределениям F, G, то для любых Т>е  Понятие Л. м. можно распространить на случай распределений в Лит.:[1] Levy P., Theorie de l'addition des variables aleatoires, P., 1937; 2 ed., P., 1954; [2] Золотарев В. М., "Тр. Матем. ин-та АН СССР", 1971, т. 112, с. 224-31; [3] 3 о л о т а р е в В. М., Сенатов В. В., "Теория вероятн. и ее примен.", 1975, т. 20, № 2, с. 239 - 50; [4] Л и н н и к Ю. В., Островский И. В., Разложения случайных величин и векторов, М., 1972. В. М. Золотарев. |
|
|
|

 функций распределения одномерных случайных величин:
функций распределения одномерных случайных величин: Введена П. Леви (см. [1]). Если между графиками функций Fи Gвписывать квадраты со сторонами, параллельными осям координат (в точках разрыва графики дополняются вертикальными отрезками), то сторона наибольшего из них равна L. Л. м. можно рассматривать как частный случай Леви- Прохорова метрики. Определение Л. м. переносится на множество Мвсевозможных неубывающих функций, заданных на
Введена П. Леви (см. [1]). Если между графиками функций Fи Gвписывать квадраты со сторонами, параллельными осям координат (в точках разрыва графики дополняются вертикальными отрезками), то сторона наибольшего из них равна L. Л. м. можно рассматривать как частный случай Леви- Прохорова метрики. Определение Л. м. переносится на множество Мвсевозможных неубывающих функций, заданных на  (при этом допускаются бесконечные значения метрики).
(при этом допускаются бесконечные значения метрики). слабую топологию. Метрич. пространство
слабую топологию. Метрич. пространство  является сепарабельным и полным. Сходимость последовательности функций из Мв метрике Lэквивалентна полной сходимости. 2) Если
является сепарабельным и полным. Сходимость последовательности функций из Мв метрике Lэквивалентна полной сходимости. 2) Если  и
и  В частности, если одна из функций, напр. G, имеет равномерно ограниченную производную, то
В частности, если одна из функций, напр. G, имеет равномерно ограниченную производную, то 