|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛЕБЕГА - СТИЛТЬЕСА ИНТЕГРАЛЗначение ЛЕБЕГА - СТИЛТЬЕСА ИНТЕГРАЛ в математической энциклопедии: обобщение Лебега интеграла. Для неотрицательной меры m название "интеграл Лебега-Стилтьеса" употребляется в том случае, когда  при условии, что оба интеграла в правой части существуют. Для нек-рой функцией Ф ограниченной вариации. В таком случае Л.- С. и. записывается в виде  Для дискретной меры Л.- С. и. представляет собой числовой ряд. Лит.:[1] Камке Е., Интеграл Лебега - Стилтьеса, пер. с нем., М., 1959. И. А. Виноградова. |
|
|
|

 и m, не есть мера Лебега; тогда интеграл определяется так же, как интеграл Лебега в общем
и m, не есть мера Лебега; тогда интеграл определяется так же, как интеграл Лебега в общем 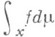 случае. Если мера m знакопеременная, то
случае. Если мера m знакопеременная, то  - неотрицательные меры, и Л.-С. и.
- неотрицательные меры, и Л.-С. и. счетная аддитивность и ограниченность меры m эквивалентна тому, что мера порождена
счетная аддитивность и ограниченность меры m эквивалентна тому, что мера порождена