ЛАПЛАСА ОПЕРАТОР

Значение ЛАПЛАСА ОПЕРАТОР в математической энциклопедии:

лапласиан,- дифференциальный оператор 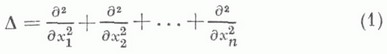определяемый формулой

(здесь - координаты в ), а также некоторые его обобщения. Л. о. (1) является простейшим эллиптич. дифференциальным оператором 2-го порядка. Л. о. играет важную роль в математич. анализе, математич. физике и геометрии (см., напр., Лапласа уравнение, Лапласа - Бельтрами уравнение, Гармоническая функция, Гармоническая форма).

Пусть Месть n-мерное риманово пространство с метрикой

пусть - матрица, обратная к матрице Тогда Л. о. (или оператор Лапласа - Бельтрами) римановой метрики (2) на Мимеет вид

где - локальные координаты на М. Оператор (1) отличается знаком от Л. о. стандартной евклидовой метрики

Обобщением оператора (3) является Л. о. на дифференциальных формах. Именно, в пространстве всех внешних дифференциальных форм на МЛ. о. имеет вид

где d - оператор внешнего дифференцирования формы, d* - формально сопряженный к dоператор, определяемый с помощью следующего произведения на гладких финитных формах:

где * - оператор Ходжа, порожденный метрикой (2) и переводящий р-формы в ( п-р )-формы. В формуле (5) формы a и b считаются действительными, на комплексных формах нужно использовать эрмитово продолжение скалярного произведения (5). Сужение оператора (4) на О-формы (т. е. функции) задается формулой (3). На р-формах при произвольном целом Л. о. в локальных координатах записывается в виде

Здесь - ковариантные производные по

- тензор кривизны, - тензор Риччи. Пусть дан произвольный эллиптич. комплекс

где Е _р - действительные или комплексные расслоения на многообразии М, Г ( Е _р) - пространства их гладких сечений. Введя в каждом расслоении Е _р эрмитову метрику, а также задав произвольным образом элемент объема на М, можно определить эрмитово скалярное произведение в пространствах гладких финитных сечений расслоений Е _р. Тогда определены операторы d*, формально сопряженные к операторам d. По формуле (3) строится Л. о. на каждом пространстве Г( Е _р). Если в качестве комплекса (6) взять комплекс де Рама, то при естественном выборе метрики в р-формах и элемента объема, порожденных метрикой (2), получается в качестве Л. о. комплекса де Рама описанный выше Л. о. на формах.

На комплексном многообразии Мнаряду с комплексом де Рама имеются эллиптич. комплексы

где - пространство гладких форм типа ( р, q).на М. Вводя эрмитову структуру в касательном расслоении на М, можно построить Л. о. (4) комплекса де Рама и Л. о. комплексов (7), (8):

Каждый из этих операторов переводит в себя пространство Если М - кэлерово многообразие, а эрмитова структура на Миндуцирована кэлеровой метрикой, то

Важным фактом, определяющим роль Л. о. эллиптич. комплекса, является существование в случае компактного многообразия Мортогонального разложения Ходжа:

В этом разложении где - Л. о. комплекса (6), так что - пространство "гармонических" сечений расслоения Е _р (в случае комплекса де Рама - это пространство всех гармонических форм степени р). Прямая сумма первых двух слагаемых в правой части формулы (9) равна а прямая сумма двух последних слагаемых совпадает с В частности, разложение (9) задает изоморфизм пространства когомологий комплекса (6) в члене и пространства гармонич. сечений

Лит.: [1] Рам Ж. д е, Дифференцируемые многообразия, пер. с франц., М., 1956; [2] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [3] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976. М. А. Шубин.