|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛАГРАНЖА УРАВНЕНИЕЗначение ЛАГРАНЖА УРАВНЕНИЕ в математической энциклопедии: - обыкновенное дифференциальное уравнение 1-го порядка, не разрешенное относительно производной, но линейное относительно независимой переменной и неизвестной функции:  Это уравнение названо по имени Ж. Лагранжа (J. Lagrange, 1759, см. [1]); уравнение (1) исследовал также Ж. Д'Аламбер (J. D'Alembert), и потому оно иногда наз. уравнением Д'Аламбера. Частным случаем Л. у. является Клеро уравнение. Л. у. всегда разрешимо в квадратурах методом введения параметра (методом дифференцирования). Пусть, напр., уравнение (1) приводится к виду 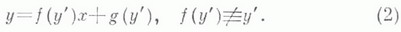 Вводя параметр р=у' и взяв полный дифференциал от обеих частей равенства (2), с учетом соотношения 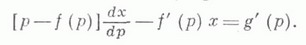 Если x=Ф( р, С) - решение этого уравнения (где С - произвольная постоянная), то решение уравнения (2) записывается в параметрич. виде 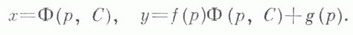 Если p0 - изолированный корень уравнения Лит.:[1] L a gr a n g e J. L., CEuvres, t. 1 , P., 1867, p. 23- 36; [2] С т е п а н о в В. В., Курс дифференциальных уравнений, 8 изд., М., 1959. Н. X. Розов. |
|
|
|
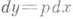приходят к линейному уравнению 1-го порядка 
то 
- также решение уравнения (2); это решение может оказаться особым.