|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛАГРАНЖА МЕТОДЗначение ЛАГРАНЖА МЕТОД в математической энциклопедии: - метод приведения квадратичной формы к сумме квадратов, указанный в 1759 Ж. Лагранжем (J. Lagrange). Пусть дана квадратичная форма 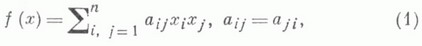 от ппеременных х 0, x1,..., х п. с коэффициентами из поля k характеристики  при помощи невырожденного линейного преобразования переменных. Л. м. состоит в следующем. Можно считать, что не все коэффициенты формы (1) равны нулю. Поэтому возможны два случая. 1) При некотором g,  где форма f1 (х).не содержит переменную xg.2) Если же все 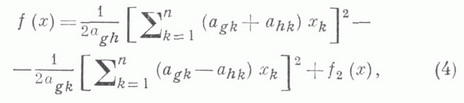 где форма f2 (х).не содержит двух переменных xg и xh. Формы, стоящие под знаками квадратов в (4), линейно независимы. Применением преобразований вида (3) и (4) форма (1) после конечного числа шагов приводится к сумме квадратов линейно независимых линейных форм. С помощью частных производных формулы (3) и (4) можно записать в виде 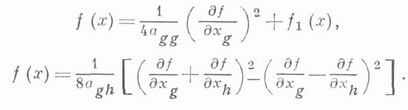 Лит.:[1] Г а н т м а х е р Ф. Р., Теория матриц, 2 изд., М., 1966; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд., М., 1975; [3] Александров П. С., Лекции по аналитической геометрии..., М., 1968. И. В. Проскуряков. |
|
|
|

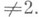 Требуется привести эту форму к канонич. виду
Требуется привести эту форму к канонич. виду 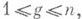 диагональный коэффициент
диагональный коэффициент 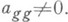 Тогда
Тогда  но
но  то
то