|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛАЗначение ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА в математической энциклопедии: форма записи многочлена степени п(интерполяционного многочлена Лагранжа), интерполирующего заданную функцию f(х).в узлах х 0, x1,..., х п:  В случае, когда значения х i являются равноотстоящими, т. е.  В выражении (2), наз. Л. и. ф. для равноотстоящих узлов, коэффициенты, стоящие перед f(х i):  наз. коэффициентами Лагранжа. Если функция f имеет производную порядка n+1 на отрезке [a, b], все узлы интерполяции лежат на этом отрезке и для любой точки то существует такая точка  где  Если абсолютная величина производной  Если узлы интерполяции - комплексные числа z0, z1 ,. . ., zn и лежат в нек-рой области G, ограниченной кусочно гладким контуром  причем  Л. и. ф. для интерполирования с помощью тригоно-метрич. полиномов наз. формула  дающая тригонометрич. полином порядка п, принимающий в заданных узлах х 0, x1,..., х п. данные значения y0, y1,..., y п. Формула предложена Ж. Лагранжем (J. Lagrange, 1795). Лит.:[1] Б е р е з и н И. С., Ж и д к о в Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С., Численные методы, 2 изд., М., 1975. Л. Д. Кудрявцев, М. К. Самарин. |
|
|
|

 с помощью обозначений (х-x0)/h=t формула (1) может быть приведена к виду
с помощью обозначений (х-x0)/h=t формула (1) может быть приведена к виду 

 что
что  ограничена на отрезке [а, b] постоянной Ми если в качестве узлов интерполяции выбраны точки, в к-рые перейдут корни многочлена Чебышева степени n+1 при линейном отображении отрезка [- 1, 1] на отрезок [а, b], то для любого
ограничена на отрезке [а, b] постоянной Ми если в качестве узлов интерполяции выбраны точки, в к-рые перейдут корни многочлена Чебышева степени n+1 при линейном отображении отрезка [- 1, 1] на отрезок [а, b], то для любого  справедливо неравенство
справедливо неравенство 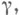 а функция f является однозначной аналитич. функцией в замыкании области G, то Л. и. ф. имеет вид
а функция f является однозначной аналитич. функцией в замыкании области G, то Л. и. ф. имеет вид