"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АРГУМЕНТА ПРИНЦИП
Значение АРГУМЕНТА ПРИНЦИП в математической энциклопедии:
геометрический принцип теории функций комплексного переменного, формулируемый следующим образом: пусть  - ограниченная область на комплексной плоскости
- ограниченная область на комплексной плоскости  , причем граница
, причем граница  является непрерывной кривой, ориентация к-рой согласована с
является непрерывной кривой, ориентация к-рой согласована с  ; если функция
; если функция  мероморфиа в окрестности
мероморфиа в окрестности  н на
н на  не имеет нулей и полюсов, то разность между числом ее нулей
не имеет нулей и полюсов, то разность между числом ее нулей  и числом полюсов
и числом полюсов  в
в  (с учетом кратностей) равна деленному на
(с учетом кратностей) равна деленному на  приращению аргумента
приращению аргумента  при положительном обходе
при положительном обходе  , т. е.
, т. е.

где  обозначает какую-либо непрерывную ветвь
обозначает какую-либо непрерывную ветвь  на кривой
на кривой 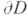 . Выражение справа равно индексу
. Выражение справа равно индексу  кривой
кривой  относительно точки
относительно точки 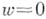 А. п. используется для доказательства различных утверждений о нулях голоморфных функций (основная теорема алгебры многочленов, теорема Гурвица о нулях и т. п.). Из А. н. следуют такие важные геометрич. принципы теории функций, как сохранения области принцип, максимума модуля принцип, теорема о локальном обращении голоморфной функции. Во многих вопросах А. п. используется неявно в виде его следствия - Руше теоремы.
А. п. используется для доказательства различных утверждений о нулях голоморфных функций (основная теорема алгебры многочленов, теорема Гурвица о нулях и т. п.). Из А. н. следуют такие важные геометрич. принципы теории функций, как сохранения области принцип, максимума модуля принцип, теорема о локальном обращении голоморфной функции. Во многих вопросах А. п. используется неявно в виде его следствия - Руше теоремы.
Имеются обобщения А. п. Условие мероморфности  в окрестности
в окрестности  можно заменить следующим:
можно заменить следующим: имеет в
имеет в  конечное число нулей и полюсов и непрерывно продолжается на
конечное число нулей и полюсов и непрерывно продолжается на  . Вместо комплексной плоскости можно рассматривать произвольную рпмаиову поверхность, при этом ограниченность
. Вместо комплексной плоскости можно рассматривать произвольную рпмаиову поверхность, при этом ограниченность  заменяется условием, что
заменяется условием, что
 - компакт. Из А. п. для римановых поверхностей следует, что на компактной римановой поверхности число нулей любой мероморфной функции, не равной тождественно нулю, равно числу полюсов. А. п. в областях на Сэквивалентен теореме о сумме логарифмических вычетов. Поэтому обобщенным А. п. иногда называют следующее утверждение. Если
- компакт. Из А. п. для римановых поверхностей следует, что на компактной римановой поверхности число нулей любой мероморфной функции, не равной тождественно нулю, равно числу полюсов. А. п. в областях на Сэквивалентен теореме о сумме логарифмических вычетов. Поэтому обобщенным А. п. иногда называют следующее утверждение. Если  мероморфна в окрестности области
мероморфна в окрестности области  , ограниченной конечным числом непрерывных кривых, и
, ограниченной конечным числом непрерывных кривых, и  на
на  не имеет нулей и полюсов, то для любой функции ф, голоморфной в окрестности
не имеет нулей и полюсов, то для любой функции ф, голоморфной в окрестности  , справедливо равенство:
, справедливо равенство:

где первая сумма распространяется на все нули, а вторая - на все полюсы f в D. Имеется топологическое обобщение А. п. (*): А. п. справедлив для любых открытых локально конечнократных отображений  непрерывно продолжающихся на
непрерывно продолжающихся на  и таких, что
и таких, что 
Аналогом А. п. для многих комплексных переменных является, напр., следующая теорема: пусть  - ограниченная область в
- ограниченная область в  с жор-дановой границей
с жор-дановой границей  и
и  есть отображение, голоморфное в окрестности
есть отображение, голоморфное в окрестности  и такое, что
и такое, что  ; тогда число прообразов 0 в
; тогда число прообразов 0 в  (с учетом кратностей) равно
(с учетом кратностей) равно  .
.
Лит.:[1] Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965; [2] IIIабат Б. В., Введение в комплексный анализ, 2 изд., ч. 2, М., 1976. Е. М. Чирка.

 - ограниченная область на комплексной плоскости
- ограниченная область на комплексной плоскости  , причем граница
, причем граница  является непрерывной кривой, ориентация к-рой согласована с
является непрерывной кривой, ориентация к-рой согласована с  ; если функция
; если функция  мероморфиа в окрестности
мероморфиа в окрестности  н на
н на  не имеет нулей и полюсов, то разность между числом ее нулей
не имеет нулей и полюсов, то разность между числом ее нулей  и числом полюсов
и числом полюсов  в
в  (с учетом кратностей) равна деленному на
(с учетом кратностей) равна деленному на  приращению аргумента
приращению аргумента  при положительном обходе
при положительном обходе  , т. е.
, т. е.
 обозначает какую-либо непрерывную ветвь
обозначает какую-либо непрерывную ветвь  на кривой
на кривой 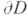 . Выражение справа равно индексу
. Выражение справа равно индексу  кривой
кривой  относительно точки
относительно точки 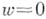 А. п. используется для доказательства различных утверждений о нулях голоморфных функций (основная теорема алгебры многочленов, теорема Гурвица о нулях и т. п.). Из А. н. следуют такие важные геометрич. принципы теории функций, как сохранения области принцип, максимума модуля принцип, теорема о локальном обращении голоморфной функции. Во многих вопросах А. п. используется неявно в виде его следствия - Руше теоремы.
А. п. используется для доказательства различных утверждений о нулях голоморфных функций (основная теорема алгебры многочленов, теорема Гурвица о нулях и т. п.). Из А. н. следуют такие важные геометрич. принципы теории функций, как сохранения области принцип, максимума модуля принцип, теорема о локальном обращении голоморфной функции. Во многих вопросах А. п. используется неявно в виде его следствия - Руше теоремы. в окрестности
в окрестности  можно заменить следующим:
можно заменить следующим: имеет в
имеет в  конечное число нулей и полюсов и непрерывно продолжается на
конечное число нулей и полюсов и непрерывно продолжается на  . Вместо комплексной плоскости можно рассматривать произвольную рпмаиову поверхность, при этом ограниченность
. Вместо комплексной плоскости можно рассматривать произвольную рпмаиову поверхность, при этом ограниченность  заменяется условием, что
заменяется условием, что  - компакт. Из А. п. для римановых поверхностей следует, что на компактной римановой поверхности число нулей любой мероморфной функции, не равной тождественно нулю, равно числу полюсов. А. п. в областях на Сэквивалентен теореме о сумме логарифмических вычетов. Поэтому обобщенным А. п. иногда называют следующее утверждение. Если
- компакт. Из А. п. для римановых поверхностей следует, что на компактной римановой поверхности число нулей любой мероморфной функции, не равной тождественно нулю, равно числу полюсов. А. п. в областях на Сэквивалентен теореме о сумме логарифмических вычетов. Поэтому обобщенным А. п. иногда называют следующее утверждение. Если  мероморфна в окрестности области
мероморфна в окрестности области  , ограниченной конечным числом непрерывных кривых, и
, ограниченной конечным числом непрерывных кривых, и  на
на  не имеет нулей и полюсов, то для любой функции ф, голоморфной в окрестности
не имеет нулей и полюсов, то для любой функции ф, голоморфной в окрестности  , справедливо равенство:
, справедливо равенство:
 непрерывно продолжающихся на
непрерывно продолжающихся на  и таких, что
и таких, что 
 - ограниченная область в
- ограниченная область в  с жор-дановой границей
с жор-дановой границей  и
и  есть отображение, голоморфное в окрестности
есть отображение, голоморфное в окрестности  и такое, что
и такое, что  ; тогда число прообразов 0 в
; тогда число прообразов 0 в  (с учетом кратностей) равно
(с учетом кратностей) равно  .
.