Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КУРАНТА - ФРИДРИХСА - ЛЕВИ УСЛОВИЕЗначение КУРАНТА - ФРИДРИХСА - ЛЕВИ УСЛОВИЕ в математической энциклопедии: - необходимое условие устойчивости разностных схем в классе бесконечно дифференцируемых коэффициентов. Пусть 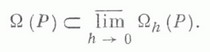 Лит.:[1] Курант Р., Фридрихе К., Л е в и Г., "Успехи матем. наук", 1940, в. 8, с. 125-60; [2] Г о д у н о в С. К., Рябенький В. С., Разностные схемы. Введение в теорию, М., 1973. Н. С. Бахвалов. |
|
|
|

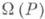 - область зависимости значения решения по какому-либо из коэффициентов (в частности, им. может быть начальное условие),
- область зависимости значения решения по какому-либо из коэффициентов (в частности, им. может быть начальное условие), 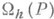 - область зависимости значения
- область зависимости значения 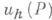 решения соответствующего разностного уравнения. Для сходимости
решения соответствующего разностного уравнения. Для сходимости 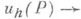
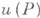 необходимо, чтобы при мельчении шага hобласть зависимости разностного уравнения покрывала область зависимости дифференциального уравнения
необходимо, чтобы при мельчении шага hобласть зависимости разностного уравнения покрывала область зависимости дифференциального уравнения