|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КУММЕРА РАСШИРЕНИЕЗначение КУММЕРА РАСШИРЕНИЕ в математической энциклопедии: расширение поля kхарактеристики  где Основной результат теории К. р. состоит в том, что для поля k, содержащего первообразный корень  Существует невырожденное спаривание Куммера, т. е. отображение  где m(n) - подгруппа группы k*, порожденная Для  Другими словами, всякий автоморфизм Пусть k - нормальное расширение поля k0 и Основные результаты о К. р. могут быть получены как следствие Гильберта теоремы о циклич. расширениях, утверждающей тривиальность одномерной группы Галуа когомологий Теория К. р. переносится на случай бесконечных абелевых расширений периода п. При этом спаривание Куммера устанавливает двойственность Понтрягина между проконечной группой G(K/k).(наделенной топологией Крулля) и дискретной группой A(K/k)(:м. [1] гл. 8, § 8; [2] гл. 3, § 2). Теория К. р., называемая также теорией Куммера, имеет аналог для случая расширений вида (1), но с п=р (так наз. теорияАртина - Шрейера). Роль группы m(n) в этом случае играет аддитивная группа простого подполя F р поля k. Основное утверждение этой теории: любое абелево расширение Кпериода рполя kимеет вид Имеется, наконец, попытка построения неабелевой "теории Куммера" [3], где роль мультипликативной группы поля играет группа матриц GL(n, К). Лит.:[1] Ленг С., Алгебра, пер. с англ., М., 1068; [2] Алгебраическая теория чисел, пер. с англ., М., 1969; [3] Таkahashi S., "J. Math. Soc. Japan", 1968, v. 20, № 1-2, p. 365 - 70. Л. В. Кузьмин. |
|
|
|

 вида
вида  п - некоторое натуральное число, причем предполагается, что поле kсодержит первообразный корень
п - некоторое натуральное число, причем предполагается, что поле kсодержит первообразный корень  из 1 степени п(в частности, пвзаимно просто с рпри
из 1 степени п(в частности, пвзаимно просто с рпри  ). К. р. названы по имени Э. Куммера (Е. Kummer), впервые подробно рассмотревшего расширения вида
). К. р. названы по имени Э. Куммера (Е. Kummer), впервые подробно рассмотревшего расширения вида 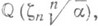 где
где  - поле рациональных чисел и
- поле рациональных чисел и 
 конечное расширение K/k является куммеровым (для данного n) тогда и только тогда, когда K/k - нормальное абелево расширение и группа Галуа
конечное расширение K/k является куммеровым (для данного n) тогда и только тогда, когда K/k - нормальное абелево расширение и группа Галуа  имеет период п. Любое К. р. поля kполностью характеризуется своей группой Куммера
имеет период п. Любое К. р. поля kполностью характеризуется своей группой Куммера  где
где  - мультипликативная группа поля k,a
- мультипликативная группа поля k,a
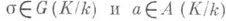 это спаривание задается формулой
это спаривание задается формулой 
 - некоторый представитель элемента а. Это спаривание определяет канонический изоморфизм
- некоторый представитель элемента а. Это спаривание определяет канонический изоморфизм  определяется своим действием на корни
определяется своим действием на корни  в (1), и это действие может быть произвольным, если только корни
в (1), и это действие может быть произвольным, если только корни  независимы. В частности, если G(K/k).- циклич. группа, то
независимы. В частности, если G(K/k).- циклич. группа, то 
 Поле Ктогда и только тогда нормально над k0, когда A(K/k).переходит в себя под действием G(K/k0)- В этом случае изоморфизм (2) является G (K/k0 )-операторным, т. е. если
Поле Ктогда и только тогда нормально над k0, когда A(K/k).переходит в себя под действием G(K/k0)- В этом случае изоморфизм (2) является G (K/k0 )-операторным, т. е. если  и
и  то
то  (Группа G(k/k0).действует на G(K/k).с помощью сопряжения в G(K/k0).).Это обстоятельство позволяет сводить многие вопросы об абелевых расширениях периода пполя kк теории К. р. даже в том случае, когда
(Группа G(k/k0).действует на G(K/k).с помощью сопряжения в G(K/k0).).Это обстоятельство позволяет сводить многие вопросы об абелевых расширениях периода пполя kк теории К. р. даже в том случае, когда  А именно, если K/k - такое расширение, то расширение
А именно, если K/k - такое расширение, то расширение  является куммеровым, причем его группа Куммера характеризуется условием: для
является куммеровым, причем его группа Куммера характеризуется условием: для  и
и  будет
будет  где i - натуральное число, определенное по модулю пусловием
где i - натуральное число, определенное по модулю пусловием 



 - корни уравнений вида xP-x=a. (см. [1] гл. 8, § 8). Существует также принадлежащее Э. Витту (Е. Witt) обобщение этой теории для случая n=ps, где s>l, использующее Витта векторы.
- корни уравнений вида xP-x=a. (см. [1] гл. 8, § 8). Существует также принадлежащее Э. Витту (Е. Witt) обобщение этой теории для случая n=ps, где s>l, использующее Витта векторы.