|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КРУГА ПРОБЛЕМАЗначение КРУГА ПРОБЛЕМА в математической энциклопедии: - проблема наилучшей асимп-тотич. оценки числа (х).целых точек ( и, v).в круге  К. Гаусс (см. [1]) доказал, что  Среднее значение для К. п.:  где С - некоторая абсолютная постоянная, К. п. по содержанию и методам исследования во многом аналогична проблеме делителей Дирихле (см. Делителей проблемы). Обобщением К. п. является проблема шара - проблема оценки В(х) - числа целых точек ( и, v, w).в шаре 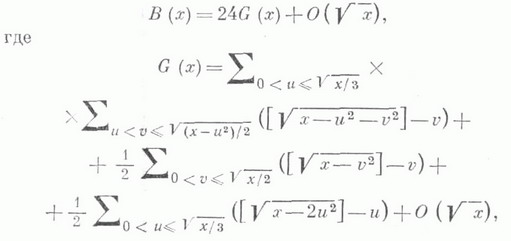 к-рая получается за счет разбиения шара шестью плоскостями  на 24 части, имеющие одинаковое число целых точек, если считать точки на плоскостях сечений с коэффициентами 1/2. Главный член роста В(х).равен объему шара 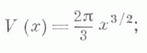 проблема сводится к оценке  Существует гипотеза, что 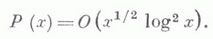 Обобщением К. п. и проблемы шара является проблема оценки  где F - положительно определенная квадратичная форма (см. [7]). Лит.:[1] G a u s s С. F., Werke, Bd 2, Gottingen, 1863, S. 269-91; [2] S i е r р i n s k i W., "Prace Mat.- Fiz.", 1906, t. 17, p. 77-118; [3] В о р о н о й Г. Ф., Собр. .соч., т. 1, К., 1952, с. 5; [4] X у а Л о - г е н, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964; [5] Виноградов И. М., "Изв. АН СССР. Сер. матем.", 1963, т. 27, № 5, с. 957-68; [6] е г о же, Особые варианты метода тригонометрических сумм, М., 1976; [7] Novak В., Lattice points in moredimensional ellipsoids, "Тр. матем. ин-та АН СССР", 1973, т. 132, с. 145 - 50. А. Ф. Лаврик. |
|
|
|

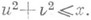 Пусть
Пусть  - нижняя грань числа а в равенстве
- нижняя грань числа а в равенстве 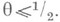 В. Серпиньский [2] по методу Г. Ф. Вороного [3] установил, что
В. Серпиньский [2] по методу Г. Ф. Вороного [3] установил, что  Последней (1982) является оценка
Последней (1982) является оценка  (см. [4]). Существует гипотеза, что остаточный член в формуле (*) есть
(см. [4]). Существует гипотеза, что остаточный член в формуле (*) есть  - любое.
- любое. Исходной для оценки является формула
Исходной для оценки является формула  - величины суммы дробных долей функций, стоящих под знаком [ ] в выражении для G(x). Наиболее глубокие оценки для Р(х).получены на основе метода тригонометрич. сумм И. М. Виноградовым [5], [6]:
- величины суммы дробных долей функций, стоящих под знаком [ ] в выражении для G(x). Наиболее глубокие оценки для Р(х).получены на основе метода тригонометрич. сумм И. М. Виноградовым [5], [6]: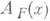 - числа целых точек в n-мерных эллипсоидах
- числа целых точек в n-мерных эллипсоидах