"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КРОНЕКЕРА СИМВОЛЗначение КРОНЕКЕРА СИМВОЛ в математической энциклопедии:
- величина  определяемая равенствами определяемая равенствами
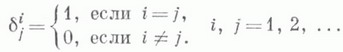 При  К. с. К. с.  имеет имеет  компонент, матрица к-рых компонент, матрица к-рых  является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866). является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866).
Обобщением К. с. является совокупность величин 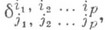 имеющих 2р целых (верхних и нижних) индексов, имеющих 2р целых (верхних и нижних) индексов,  равных +1 (или -1), если строка индексов равных +1 (или -1), если строка индексов  - четная (нечетная) перестановка строки различных индексов (j1, j2, ..., j р), и нулю - во всех остальных случаях. Числа - четная (нечетная) перестановка строки различных индексов (j1, j2, ..., j р), и нулю - во всех остальных случаях. Числа  (часто обозначаемые при (часто обозначаемые при  через) наз. компонентами К. с. Аффинный через) наз. компонентами К. с. Аффинный  тензор типа ( р, р), имеющий в нек-ром базисе компоненты, равные компонентам К. с., имеет те же самые компоненты в любом другом базисе. тензор типа ( р, р), имеющий в нек-ром базисе компоненты, равные компонентам К. с., имеет те же самые компоненты в любом другом базисе.
К. с. удобен в различных задачах тензорного исчисления. Напр., определитель
 равен сумме
 в к-рой суммирование производится по всем  перестановкам чисел 1, 2, . . . , п. Операция альтернирования тензора перестановкам чисел 1, 2, . . . , п. Операция альтернирования тензора  имеет вид имеет вид
 Лит.:[1] Kronecker L., Vorlesungen fiber die Theorie der Determinanten, Lpz., 1903. Л. Я. Купцов.
|
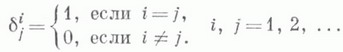




 определяемая равенствами
определяемая равенствами  К. с.
К. с.  имеет
имеет  компонент, матрица к-рых
компонент, матрица к-рых  является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866).
является единичной. К. с. введен Л. Кронекером (L. Kronecker, 1866).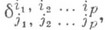 имеющих 2р целых (верхних и нижних) индексов,
имеющих 2р целых (верхних и нижних) индексов,  равных +1 (или -1), если строка индексов
равных +1 (или -1), если строка индексов  - четная (нечетная) перестановка строки различных индексов (j1, j2, ..., j р), и нулю - во всех остальных случаях. Числа
- четная (нечетная) перестановка строки различных индексов (j1, j2, ..., j р), и нулю - во всех остальных случаях. Числа  (часто обозначаемые при
(часто обозначаемые при  через) наз. компонентами К. с. Аффинный
через) наз. компонентами К. с. Аффинный  тензор типа ( р, р), имеющий в нек-ром базисе компоненты, равные компонентам К. с., имеет те же самые компоненты в любом другом базисе.
тензор типа ( р, р), имеющий в нек-ром базисе компоненты, равные компонентам К. с., имеет те же самые компоненты в любом другом базисе. перестановкам чисел 1, 2, . . . , п. Операция альтернирования тензора
перестановкам чисел 1, 2, . . . , п. Операция альтернирования тензора  имеет вид
имеет вид