|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
КРИСТАЛЛОГРАФИЧЕСКАЯ ГРУППАЗначение КРИСТАЛЛОГРАФИЧЕСКАЯ ГРУППА в математической энциклопедии: дискретная группа движений n-мерного евклидова пространства Е п, имеющая ограниченную фундаментальную область. Две К. г. считаются эквивалентными, если они сопряжены в группе аффинных преобразований пространства Е п. Происхождение теории К. г. связано с изучением симметрии орнаментов ( п=2).и кристаллических структур (n=3). Классификация всех плоских (двумерных) и пространственных (трехмерных) К. г. была получена в конце 19 в. Е. С. Федоровым ц несколько позже А. Шёнфлисом (см. [2], [3], а также [6], [7], [9]). С точностью до эквивалентности имеется 17 плоских и 219 пространственных К. г.; если же рассматривать пространственные группы с точностью до сопряженности при помощи аффинных преобразований, сохраняющих ориентацию, то их будет 230. В 1910 Л. Бибербахом были исследованы К. г. в произвольной размерности [4]. Он доказал, в частности, следующие теоремы. 1) Всякая re-мерная К. г. Г содержит плинейно независимых параллельных переносов; группа Gлинейных частей преобразований из Г конечна. (Для n=3 это было доказано в [3].) 2) Две К. г. эквивалентны тогда и только тогда, когда они изоморфны как абстрактные группы. 3) При любом пимеется лишь конечное число n-мерных К. г., рассматриваемых с точностью до эквивалентности (что является решением 18-й проблемы Гильберта). Теорема 1) позволяет дать следующее описание строения К. г. как абстрактных групп. Пусть L - совокупность всех параллельных переносов, принадлежащих К. г. Г. Тогда L - нормальная подгруппа конечного индекса, изоморфная Группа G линейных частей К. г. Г сохраняет решетку L', иными словами, в базисе решетки Lпреобразования из G записываются целочисленными матрицами. Для того чтобы задать К. г. Г, нужно, помимо G и L, указать для каждого Любая тройка  где Двум классам когомологий отвечают эквивалентные К. г. тогда и только тогда, когда они переводятся друг в друга нормализатором группы G в  является изоморфизмом. Это легко может быть выведено из точной последовательности когомологий группы G. Две К. г. относятся к одному классу (соответственно арифметическому классу), если их группы линейных частей сопряжены в Среди конечных групп целочисленных матриц можно выделить группы симметрии решеток, т. е. группы всех ортогональных преобразований, сохраняющих какую-либо заданную решетку в векторном пространстве (и записанных в базисе этой решетки). В 1848 О. Браве (A. Bravais) определил все возможные группы симметрии 3-мерных решеток и разбил в соответствии с этим все 3-мерные решетки на 14 типов (так наз. типы Браве). Подгруппы группы Подгруппы Браве можно интерпретировать также как стационарные подгруппы для естественного действия группы Приводимая таблица дает число конечных подгрупп в группе
Пересечение подгрупп Браве также есть подгруппа Браве. Наименьшая подгруппа Браве Линейные представления К. г. Неприводимые конечномерные комплексные линейные представления К. г. Г описываются следующим образом. Пусть  и s - такое неприводимое представление группы Лит.:[1] Браве О., Избр. научные труды, Л., 1974, с. 41 -138; [2] Ф е д о р о в Е. С., Симметрия и структура кристаллов. Основные работы, М., 1949, с. 111 - 255; [3] Sсhоеnflies A., Kristallsysteme und Kristallstruktur, Lpz., 1891; [4] В i e b e r-b а с h L., "Math. Ann.", 1911, Bd 70, S. 297-336; 1912, Bd 72, S. 400-12: [5] Д е л о H e Б., Па Дуров Н., Александров А., Математические основы структурного анализа кристаллов..., Л.- М., 1934; [6] Шубников А. В., Атлас кристаллографических групп симметрии, М.-Л., 194В; [7] Zassenhaus H., "Comm. math, hclv.", 1948, v. 21, p. 117 - 141; [8] М а л ь ц е в А. И., Избр. труды, т. 1- Классическая алгебра, М., 1976, с. 371-75; [9] Л ю б а р с к и й Г. Я., Теория групп и ее применение в физике, М., 1957; [10] Фаддеев Д. К., Таблицы основных унитарных представлений федоровских групп, М.- Л., 1961; [11] Делоне Б. Н., Галиулин Р. В., Штогрин М. И., в кн.: РГгоги науки и техники. Современные проблемы математики, т. 2, М., 1973, с. 119 - 254. Э. Б. Винберг. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||

 и совпадающая со своим централизатором в Г. Наличие такой нормальной подгруппы Lв абстрактной группе Г является и достаточным условием того, чтобы группа Г была изоморфна К. г. [7].
и совпадающая со своим централизатором в Г. Наличие такой нормальной подгруппы Lв абстрактной группе Г является и достаточным условием того, чтобы группа Г была изоморфна К. г. [7]. такой вектор a(g), что преобразование
такой вектор a(g), что преобразование  принадлежит группе Г. Вектор a(g).определен с точностью до прибавления вектора из L. Отображение
принадлежит группе Г. Вектор a(g).определен с точностью до прибавления вектора из L. Отображение  является одномерным коциклом на Gсо значениями в V/L, где V - векторное пространство, ассоциированное с Е п.
является одномерным коциклом на Gсо значениями в V/L, где V - векторное пространство, ассоциированное с Е п. - конечная линейная группа, L -G-инвариантная решетка и а - одномерный коцикл на G со значениями в V/L, соответствует указанным образом нек-рой К. г. При этом тройки
- конечная линейная группа, L -G-инвариантная решетка и а - одномерный коцикл на G со значениями в V/L, соответствует указанным образом нек-рой К. г. При этом тройки  - когомологичные коциклы, соответствуют эквивалентным К. г. Нулевому классу когомологпй соответствует расщепляемая (или с и м м о р ф н а я) К. г., к-рая, при подходящем выборе начала отсчета, состоит из всех преобразований вида
- когомологичные коциклы, соответствуют эквивалентным К. г. Нулевому классу когомологпй соответствует расщепляемая (или с и м м о р ф н а я) К. г., к-рая, при подходящем выборе начала отсчета, состоит из всех преобразований вида 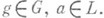 В матричной интерпретации описание всех n-мерных К. г. сводится к описанию всех конечных групп целочисленных матриц порядка п(с точностью до сопряженности в группе
В матричной интерпретации описание всех n-мерных К. г. сводится к описанию всех конечных групп целочисленных матриц порядка п(с точностью до сопряженности в группе  ) и, для каждой такой группы G, к вычислению группы когомологий
) и, для каждой такой группы G, к вычислению группы когомологий 
 Теорема 2) Бибербаха и результат X. Цассенхауза [7] означают, что естественный гомоморфизм
Теорема 2) Бибербаха и результат X. Цассенхауза [7] означают, что естественный гомоморфизм  (соответственно в
(соответственно в 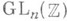 ). При ге=3 имеется 32 класса и 73 арифметических класса К. г.
). При ге=3 имеется 32 класса и 73 арифметических класса К. г. являющиеся группами симметрии решеток, наз. подгруппами Браве.
являющиеся группами симметрии решеток, наз. подгруппами Браве. на множестве положительно определенных квадратичных форм от n переменных. Поэтому для их нахождения может быть использована теория приведения (см. [11]). Всякая максимальная конечная подгруппа группы
на множестве положительно определенных квадратичных форм от n переменных. Поэтому для их нахождения может быть использована теория приведения (см. [11]). Всякая максимальная конечная подгруппа группы  является подгруппой Браве (но не наоборот).
является подгруппой Браве (но не наоборот). (рассматриваемых с точностью до сопряженности).
(рассматриваемых с точностью до сопряженности). содержащая группу G линейных частей К. г. Г и рассматриваемая с точностью до сопряженности в
содержащая группу G линейных частей К. г. Г и рассматриваемая с точностью до сопряженности в  (соответственно в
(соответственно в  ), наз. геометрической (соответственно арифметической) голоэдрией группы Г. Если Г - К. г. общего положения в том смысле, что ее нельзя аффинным преобразованием перевести в К. г., решетка параллельных переносов к-рой обладает меньшей симметрией, то
), наз. геометрической (соответственно арифметической) голоэдрией группы Г. Если Г - К. г. общего положения в том смысле, что ее нельзя аффинным преобразованием перевести в К. г., решетка параллельных переносов к-рой обладает меньшей симметрией, то  совпадает с группой симметрии решетки параллельных переносов группы Г. Две К. г. относятся к одной сингонии (соответственно типу Браве), если их геометрические (соответственно арифметические) голоэдрии совпадают. При n=3 имеется 7 сингонии и 14 типов Браве кристаллографич. групп.
совпадает с группой симметрии решетки параллельных переносов группы Г. Две К. г. относятся к одной сингонии (соответственно типу Браве), если их геометрические (соответственно арифметические) голоэдрии совпадают. При n=3 имеется 7 сингонии и 14 типов Браве кристаллографич. групп. - какой-либо характер (гомоморфизм в мультипликативную группу комплексных чисел) группы L,
- какой-либо характер (гомоморфизм в мультипликативную группу комплексных чисел) группы L, что
что  при
при  Тогда представление группы Г, индуцированное представлением s подгруппы
Тогда представление группы Г, индуцированное представлением s подгруппы  (см. Индуцированное представление), неприводимо. Всякое неприводимое представление группы Г получается описанным способом (см. [9], [10]).
(см. Индуцированное представление), неприводимо. Всякое неприводимое представление группы Г получается описанным способом (см. [9], [10]).